题目内容
10. 如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系
如图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠ACB=90°,棱AA1=2,如图,以C为原点,分别以CA,CB,CC1为x,y,z轴建立空间直角坐标系(1)求平面A1B1C的法向量;
(2)求直线AC与平面A1B1C夹角的正弦值.
分析 (1)求出平面中的两个共点向量,利用数量积为0,求出平面A1B1C的法向量;
(2)求出$\overrightarrow{CA}=(1,0,0)$,利用向量的夹角公式求直线AC与平面A1B1C夹角的正弦值.
解答  解:(1)由题意可知C(0,0,0),A1(1,0,2),B1(0,1,2)
解:(1)由题意可知C(0,0,0),A1(1,0,2),B1(0,1,2)
故$\overrightarrow{C{A_1}}=(1,0,2),\overrightarrow{C{B_1}}=(0,1,2)$…(3分)
设$\overrightarrow v=({{x_0},{y_0},{z_0}})$为平面A1B1C的法向量,则$\overrightarrow v•\overrightarrow{C{A_1}}=({{x_0},{y_0},{z_0}})(1,0,2)={x_0}+2{z_0}=0$,…(5分)$\overrightarrow v•\overrightarrow{C{B_1}}=({{x_0},{y_0},{z_0}})(0,1,2)={y_0}+2{z_0}=0$…(7分)
$\left\{{\begin{array}{l}{{x_0}=-2{z_0}}\\{{y_0}=-2{z_0}}\end{array}}\right.$,令z0=1,则$\overrightarrow v=({-2,-2,1})$…(9分)
(2)设直线AC与平面A1B1C夹角为θ,$\overrightarrow{CA}=(1,0,0)$…(10分)
sinθ=$\frac{|-2|}{1×\sqrt{4+4+1}}$=$\frac{2}{3}$…(14分)
点评 本小题主要考查求平面的法向量,以及直线与平面所成的角,考查空间想象能力、运算能力和推理论证能力.属中档题.正确运用向量法是关键.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 一个楔子形状几何体的直观图如图所示,其底面ABCD为一个矩形,其中AB=6,AD=4,顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6$\sqrt{2}$,二面角F-BC-A的余弦值为$\frac{\sqrt{17}}{17}$.设M,N分别是AD,BC的中点.
一个楔子形状几何体的直观图如图所示,其底面ABCD为一个矩形,其中AB=6,AD=4,顶部线段EF∥平面ABCD,棱EA=ED=FB=FC=6$\sqrt{2}$,二面角F-BC-A的余弦值为$\frac{\sqrt{17}}{17}$.设M,N分别是AD,BC的中点. 如图所示为一简单组合体,其底面ABCD为直角梯形,AD⊥CD,AB∥CD,PD⊥平面ABCD,PD∥EC,PD=CD=2AD=2AB=2,CE=1
如图所示为一简单组合体,其底面ABCD为直角梯形,AD⊥CD,AB∥CD,PD⊥平面ABCD,PD∥EC,PD=CD=2AD=2AB=2,CE=1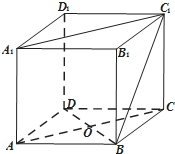 在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点. 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,PD=AD=DC=2AB,则异面直线PC与AB所成角的大小为$\frac{π}{4}$;直线PB与平面PDC所成角的正弦值为$\frac{2}{3}$.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,PD=AD=DC=2AB,则异面直线PC与AB所成角的大小为$\frac{π}{4}$;直线PB与平面PDC所成角的正弦值为$\frac{2}{3}$. 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.