题目内容
已知向量 =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), =(sinωx,1)(其中ω>0),令f(x)=
=(sinωx,1)(其中ω>0),令f(x)= ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求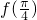 的值;
的值;
(2)写出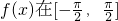 上的单调递增区间.
上的单调递增区间.
解:(1)f(x)= =2cosωxsinωx+cos2ωx
=2cosωxsinωx+cos2ωx
=sin2ωx+cos2ωx
=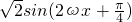 .
.
∵f(x)的最小正周期为π,∴ω=1.
∴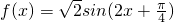 .
.
∴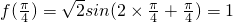 .(6分)
.(6分)
(2)∵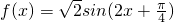 ,
,
∴当-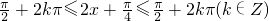 ,
,
即-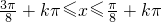 (k∈Z)时,f(x)单调递增,
(k∈Z)时,f(x)单调递增,
∵ ,
,
∴f(x)在 上的单调递增区间为
上的单调递增区间为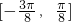 .(13分)
.(13分)
分析:(1)把向量 =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), =(sinωx,1)代入f(x)=
=(sinωx,1)代入f(x)= ,利用二倍角公式和两角和的正弦函数化为:
,利用二倍角公式和两角和的正弦函数化为: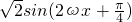 ,根据周期求出ω,然后求解
,根据周期求出ω,然后求解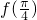 的值;
的值;
(2)利用正弦函数的单调增区间求出函数f(x)的单调增区间,选择适当的k值求出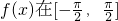 上的单调递增区间.
上的单调递增区间.
点评:本题是基础题,考查向量的数量积,二倍角和两角和的正弦函数的化简,三角函数的单调增区间的求法,考查计算能力,是常考题型.
 =2cosωxsinωx+cos2ωx
=2cosωxsinωx+cos2ωx=sin2ωx+cos2ωx
=
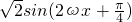 .
.∵f(x)的最小正周期为π,∴ω=1.
∴
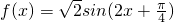 .
.∴
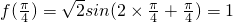 .(6分)
.(6分)(2)∵
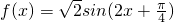 ,
,∴当-
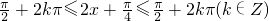 ,
,即-
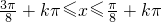 (k∈Z)时,f(x)单调递增,
(k∈Z)时,f(x)单调递增,∵
 ,
,∴f(x)在
 上的单调递增区间为
上的单调递增区间为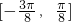 .(13分)
.(13分)分析:(1)把向量
 =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), =(sinωx,1)代入f(x)=
=(sinωx,1)代入f(x)= ,利用二倍角公式和两角和的正弦函数化为:
,利用二倍角公式和两角和的正弦函数化为: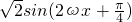 ,根据周期求出ω,然后求解
,根据周期求出ω,然后求解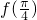 的值;
的值;(2)利用正弦函数的单调增区间求出函数f(x)的单调增区间,选择适当的k值求出
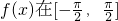 上的单调递增区间.
上的单调递增区间.点评:本题是基础题,考查向量的数量积,二倍角和两角和的正弦函数的化简,三角函数的单调增区间的求法,考查计算能力,是常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目