题目内容
7.已知函数f(x)=loga(x+1),g(x)=loga(1-x),其中(a>0且a≠1).(1)求函数h(x)=f(x)-g(x)的定义域,并证明h(x)的奇偶性;
(2)根据复合函数单调性理论判断g(x)的单调性,并说明理由.
分析 (1)求出h(x)=loga(x+1)-loga(1-x),要使h(x)有意义,则$\left\{\begin{array}{l}{x+1>0}\\{1-x>0}\end{array}\right.$,这样即可得出h(x)的定义域,而求h(-x)=-h(x),从而得出h(x)为奇函数;
(2)可令1-x=u,u>0,从而得出函数u=1-x单调递减,讨论a>1,和0<a<1,从而判断y=logau的单调性,这样根据复合函数的单调性便可得出g(x)的单调性.
解答 解:(1)h(x)=loga(x+1)-loga(1-x);
解$\left\{\begin{array}{l}{x+1>0}\\{1-x>0}\end{array}\right.$得,-1<x<1;
∴h(x)的定义域为(-1,1);
h(-x)=loga(1-x)-loga(1+x)=-h(x);
∴函数h(x)为奇函数;
(2)令u=1-x,u>0,则u在(-∞,1)上单调递减;
当a>1时,函数y=logau在定义域内单调递增,当0<a<1时,函数y=logau在定义域内单调递减;
∴当a>1时,函数g(x)在(-∞,1)上单调递减,当0<a<1时,函数g(x)在(-∞,1)上单调递增.
点评 考查函数定义域的概念,奇函数的定义及判断方法,一次函数、对数函数的单调性,以及复合函数的单调性的判断.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列函数中,是奇函数且在区间(0,1)内单调递减的函数是( )
| A. | y=log${\;}_{\frac{1}{2}}$x | B. | $y=\frac{-1}{x}$ | C. | y=-x3 | D. | y=tanx |
2.下列函数,在其定义域内既是奇函数又是增函数的是( )
| A. | y=-log2x | B. | y=3x | C. | y=-$\frac{1}{x}$ | D. | y=x3 |
16.如图所示,是某小朋友在用火柴拼图时呈现的图形,其中第1个图形用了3根火柴,第2个图形用了9根火柴,第3个图形用了18个火柴,…,第2014个图形用的火柴根数为( )


| A. | 2012×2015 | B. | 2013×2014 | C. | 2013×2015 | D. | 3021×2015 |
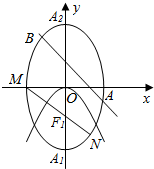 如图,M为椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,F1是它的下焦点,F1也是抛物线x2=-4y的焦点,直线MF1与椭圆C的另一个交点为N,满足$\overrightarrow{M{F}_{1}}$=$\frac{5}{3}$$\overrightarrow{{F}_{1}N}$
如图,M为椭圆C:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点,F1是它的下焦点,F1也是抛物线x2=-4y的焦点,直线MF1与椭圆C的另一个交点为N,满足$\overrightarrow{M{F}_{1}}$=$\frac{5}{3}$$\overrightarrow{{F}_{1}N}$