题目内容
(14分)己知![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() :
:![]() (
(![]() )上的三点,其中点
)上的三点,其中点![]() 的坐标为
的坐标为![]() ,
,![]() 过椭圆的中心,且
过椭圆的中心,且![]() ,
,![]() 。
。
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() (斜率存在时)与椭圆
(斜率存在时)与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,设
,设![]() 为椭圆
为椭圆![]() 与
与![]() 轴负半轴的交点,且
轴负半轴的交点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解析:(Ⅰ)∵![]() 且
且![]() 过
过![]() ,则
,则![]() .…………2分
.…………2分
∵![]() ,
,
∴![]() ,即
,即![]() .…………………………………4分
.…………………………………4分
又∵![]() ,设椭圆
,设椭圆![]() 的方程为
的方程为![]() ,
,
将C点坐标代入得![]() ,
,
解得![]() ,
,![]() .
.
∴椭圆![]() 的方程为
的方程为![]() . …………………………………6分
. …………………………………6分

(Ⅱ)由条件![]() ,
,
当![]() 时,显然
时,显然![]() ;……………………………………………………8分
;……………………………………………………8分
当![]() 时,设
时,设![]() :
:![]() ,
,
 ,消
,消![]() 得
得![]()
由![]() 可得,
可得,![]() ……①………………………………………10分
……①………………………………………10分
设![]() ,
,![]() ,
,![]() 中点
中点![]() ,
,
则![]() ,
,![]()
∴![]() .…………………………………12分
.…………………………………12分
由![]() ,
,
∴![]() ,即
,即![]() 。
。
∴ ,化简得
,化简得![]() ……②
……②
∴![]()
将①代入②得,![]() 。
。
∴![]() 的范围是
的范围是![]() 。
。

练习册系列答案
相关题目
 满足:
满足: ,
,
 ,求证
,求证 是等比数列,并求其通项公式;
是等比数列,并求其通项公式; 满足:
满足: ,
,
 ,求证
,求证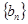 是等比数列,并求其通项公式;
是等比数列,并求其通项公式;