题目内容
已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成角为
,且侧面ABB1A1⊥底面ABC.
(1)证明:点B1在平面ABC上的射影O为AB的中点;
(2)求二面角C-AB1-B的大小.
| π | 3 |
(1)证明:点B1在平面ABC上的射影O为AB的中点;
(2)求二面角C-AB1-B的大小.
分析:(1)过B1点作B1O⊥BA于点O.由面面垂直的性质定理,可得B1O⊥面ABC,所以∠B1BA是侧面BB1与底面ABC所成的角,∠B1BO=
.在Rt△B1OB中,BO=BB1cos
=1=
AB,所以O是AB的中点,即点B1在平面ABC上的射影O为AB的中点;
(2)连接AB1,过点O作OM⊥AB1,连线CM、OC.正三角形ABC的中线OC⊥AB,结合平面ABC⊥平面AA1BB1,得到OC⊥平面AA1B1B,结合三垂线定理可得AB1⊥CM,所以∠OMC是二面角C-AB1-B的平面角.最后在在Rt△OCM中求出OC、OM的长,利用直角三角形三角函数的定义,可得tan∠OMC=2,即得二面角C-AB1-B的大小为arctan2.
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
(2)连接AB1,过点O作OM⊥AB1,连线CM、OC.正三角形ABC的中线OC⊥AB,结合平面ABC⊥平面AA1BB1,得到OC⊥平面AA1B1B,结合三垂线定理可得AB1⊥CM,所以∠OMC是二面角C-AB1-B的平面角.最后在在Rt△OCM中求出OC、OM的长,利用直角三角形三角函数的定义,可得tan∠OMC=2,即得二面角C-AB1-B的大小为arctan2.
解答:解:(1)过B1点作B1O⊥BA于点O.
∵侧面ABB1A1⊥底面ABC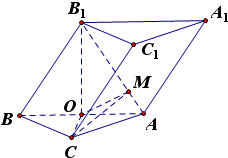 ,侧面ABB1A1∩底面ABC=AB,
,侧面ABB1A1∩底面ABC=AB,
∴B1O⊥面ABC,
∴∠B1BA是侧面BB1与底面ABC所成的角,可得∠B1BO=
在Rt△B1OB中,BB1=2,∴BO=BB1cos
=1
又∵BB1=AB=2,∴BO=
AB
∴O是AB的中点,可得点B1在平面ABC上的射影O为AB的中点…(6分)
(2)连接AB1,过点O作OM⊥AB1,连线CM、OC,
∵正三角形ABC中,O是AB的中点,∴OC⊥AB,
∵平面ABC⊥平面AA1BB1,平面ABC∩平面AA1BB1=AB
∴OC⊥平面AA1B1B,可得OM是斜线CM在平面AA1B1B的射影
∵OM⊥AB1,∴AB1⊥CM,可得∠OMC是二面角C-AB1-B的平面角
∵等边三角形ABC中,OC=BCsin60°=
.Rt△AOB1中,OM=OAsin60°=
,
∴在Rt△OCM中,tan∠OMC=
=2,可得∠OMC=arctan2.
∴二面角C-AB1-B的大小为arctan2.…(12分)
∵侧面ABB1A1⊥底面ABC
 ,侧面ABB1A1∩底面ABC=AB,
,侧面ABB1A1∩底面ABC=AB,∴B1O⊥面ABC,
∴∠B1BA是侧面BB1与底面ABC所成的角,可得∠B1BO=
| π |
| 3 |
在Rt△B1OB中,BB1=2,∴BO=BB1cos
| π |
| 3 |
又∵BB1=AB=2,∴BO=
| 1 |
| 2 |
∴O是AB的中点,可得点B1在平面ABC上的射影O为AB的中点…(6分)
(2)连接AB1,过点O作OM⊥AB1,连线CM、OC,
∵正三角形ABC中,O是AB的中点,∴OC⊥AB,
∵平面ABC⊥平面AA1BB1,平面ABC∩平面AA1BB1=AB
∴OC⊥平面AA1B1B,可得OM是斜线CM在平面AA1B1B的射影
∵OM⊥AB1,∴AB1⊥CM,可得∠OMC是二面角C-AB1-B的平面角
∵等边三角形ABC中,OC=BCsin60°=
| 3 |
| ||
| 2 |
∴在Rt△OCM中,tan∠OMC=
| OC |
| OM |
∴二面角C-AB1-B的大小为arctan2.…(12分)
点评:本题给出特殊的三棱柱,证明直线与平面垂直并求平面与平面所成的角,着重考查了平面与平面垂直的性质和二面角的平面角及求法等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C是边长为2的菱形,∠B1BC=60°,侧面BB1C1C⊥底面ABC,∠ABC=90°,二面角A-B1B-C为30°. 已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点.
已知斜三棱柱ABC-A1B1C1的侧面BB1C1C与底面ABC垂直,BB1=BC,∠B1BC=60°,AB=AC,M是B1C1的中点. 如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为
如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为 已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl
已知斜三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC,A1B⊥ACl