Question

已知斜三棱柱ABC-A₁B₁C₁的侧面BB₁C₁C是边长为2的菱形，∠B₁BC=60°，侧面BB₁C₁C⊥底面ABC，∠ABC=90°，二面角A-B₁B-C为30°．
（1）求证：AC⊥平面BB₁C₁C；
（2）求AB₁与平面BB₁C₁C所成角的正切值．

Answer 1

分析：（1）由平面BB₁C₁C⊥平面ABC且平面BB₁C₁C∩平面ABC=BC，AC⊥BC，由面面垂直的性质定理可得AC⊥平面BB₁C₁C
（2）由（1）知AC⊥平面BB₁C₁C，则有∠AB₁C为AB₁与平面BB₁C₁C所成的角，连接B₁C，则∠AB₁C为AB₁与平面BB₁C₁C所成的角，在Rt△ACB₁中可求得tan∠∠AB₁C．

解答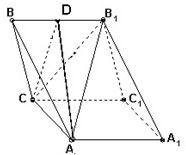：证明：（1）∵平面BB₁C₁C⊥平面ABC
平面BB₁C₁C∩平面ABC=BC
又∵AC⊥BC，AC?平面ABC
∴AC⊥平面BB₁C₁C（6分）
（2）取BB₁的中点D，
AC⊥平面BB₁C₁C
∴AC⊥BB₁
∴BB₁⊥平面ADC
∴AD⊥BB₁
∴∠CDA为二面角A-BB₁-C的平面角
∴∠CDA=30°
∵CD=

3

∴AC=1（8分）
连接B₁C，则∠AB₁C为AB₁与平面BB₁C₁C所成的角（10分）
在Rt△ACB₁中tan∠AB₁C=

AC

B1C

=

1

2

（12分）

点评：本题主要考查线线垂直，线面垂直，面面垂直的转化及在求线面角，二面角中的应用．