题目内容
已知函数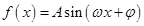 ,x∈R(其中A>0,ω>0,
,x∈R(其中A>0,ω>0, )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M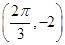 .
.
(1)求f(x)的解析式;
(2)当x∈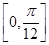 时,求f(x)的最大值.
时,求f(x)的最大值.
存在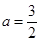 符合题意.
符合题意.
解析试题分析:将原函数化简为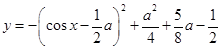 ,令
,令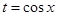 ,0≤t≤1,可将问题转化为一元二次函数中来解决,
,0≤t≤1,可将问题转化为一元二次函数中来解决,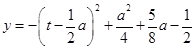 ,其中0≤t≤1,对称轴
,其中0≤t≤1,对称轴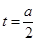 与给定的范围
与给定的范围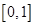 进行讨论,得出最值,验证最值是否取到1 即可.
进行讨论,得出最值,验证最值是否取到1 即可.
解: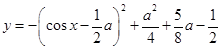 ,
,
当0≤x≤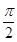 时,0≤cos x≤1,令
时,0≤cos x≤1,令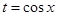 则0≤t≤1,
则0≤t≤1,
∴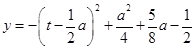 ,0≤t≤1.
,0≤t≤1.
当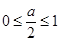 ,即0≤a≤2时,则当
,即0≤a≤2时,则当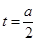 ,即
,即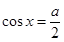 时.
时.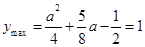 ,解得
,解得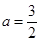 或a=-4(舍去).
或a=-4(舍去).
当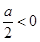 ,即a<0时,则当t=0,即
,即a<0时,则当t=0,即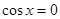 时,
时, ,解得
,解得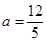 (舍去).
(舍去).
当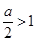 ,即a>2时,则当t=1,即
,即a>2时,则当t=1,即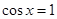 时,
时,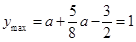 ,解得
,解得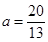 (舍去).
(舍去).
综上知,存在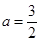 符合题意.
符合题意.
考点:同角三角函数的基本关系式,二次函数求最值.

练习册系列答案
相关题目
 .
.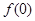 的值;
的值; ,求
,求 的值.
的值. ,
, .
. ,求
,求 的最大值及相应的
的最大值及相应的 的取值集合;
的取值集合; 是
是 ,求
,求 的值和
的值和 ,
, .
. 值; (2)求
值; (2)求 的值.
的值. 直线
直线 是
是 图像的任意两条对称轴,且
图像的任意两条对称轴,且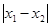 的最小值为
的最小值为 .
. 的单调增区间;
的单调增区间;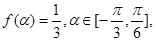 求
求 的值;
的值; 的方程
的方程 在
在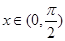 有实数解,求实数
有实数解,求实数 的取值.
的取值. ,
, .
. 的最小正周期和单调增区间;
的最小正周期和单调增区间; 上的最小值和最大值;
上的最小值和最大值; ,求使
,求使 的
的 取值范围.
取值范围. 各取何值时,扇形的面积S最大?并求出扇形面积的最大值.
各取何值时,扇形的面积S最大?并求出扇形面积的最大值.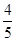 ,求S△AOB.
,求S△AOB.