题目内容
10.已知函数f(x)满足f(x)=f($\frac{1}{x}$),当x∈[1,3]时,f(x)=lnx,若在区间[$\frac{1}{3}$,3]内,曲线g(x)=f(x)-ax与x轴有三个不同的交点,则实数a的取值范围是( )| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | D. | [$\frac{ln3}{3}$,$\frac{1}{2e}$) |
分析 作出函数的图象,结合函数的图象解答即可.
解答 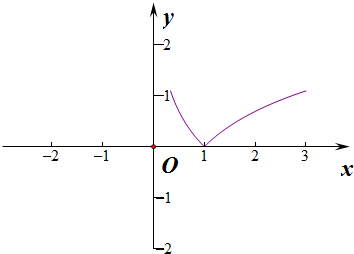 解:设x∈[$\frac{1}{3}$,1],
解:设x∈[$\frac{1}{3}$,1],
则$\frac{1}{x}$∈[1,3]时,
又f(x)=f($\frac{1}{x}$)=ln($\frac{1}{x}$)=-lnx,
∴函数f(x)的图象如图所示:
当a≤0时,显然,不合乎题意,
当a>0时,如图示,
当x∈($\frac{1}{3}$,1]时,存在一个零点,
当1<x<3时,f(x)=lnx,
可得g(x)=lnx-ax,(x∈(1,3])
g′(x)=$\frac{1}{x}$-a=$\frac{1-ax}{x}$,
若g′(x)<0,可得x>$\frac{1}{a}$,g(x)为减函数,
若g′(x)>0,可得x<$\frac{1}{a}$,g(x)为增函数,
此时f(x)必须在[1,3]上有两个零点,
∴$\left\{\begin{array}{l}{g(\frac{1}{a})>0}\\{g(3)≤0}\\{g(1)≤0}\end{array}\right.$
解得,$\frac{ln3}{3}≤a<\frac{1}{e}$.
故选C.
点评 本题重点考查函数的零点,属于中档题,难度中等.

练习册系列答案
相关题目
20.在棱长为3的正方体ABCD-A1B1C1D1中,P在线段BD1上,且$\frac{BP}{P{D}_{1}}=\frac{1}{2}$,M为线段B1C1上的动点,则三棱锥M-PBC的体积为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{9}{2}$ | D. | 与M点的位置有关 |
 如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2AD=2,E为AB的中点,F为D1E上的一点,D1F=2FE.
如图,在长方体ABCD-A1B1C1D1中,AA1=AB=2AD=2,E为AB的中点,F为D1E上的一点,D1F=2FE.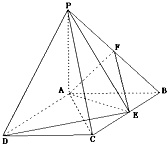 如图四棱锥P-ABCD中PA⊥平面ABCD,底面ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,点E在边BC上移动.
如图四棱锥P-ABCD中PA⊥平面ABCD,底面ABCD是矩形,PA=AB=1,∠PDA=30°,点F是PB的中点,点E在边BC上移动.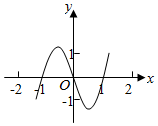 已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象大致是( )
已知函数y=xf′(x)的图象如图所示(其中f′(x)是函数f(x)的导函数),下面四个图象中,y=f(x)的图象大致是( )