题目内容
在复平面上,一个正方形的四个顶点按照逆时针方向依次为Z1,Z2,Z3,O (其中O是原点),已知Z2对应复数Z2=1+| 3 |
分析:由复数的三角形式和辐角主值可直接求解.
解答:本小题主要考查复数基本概念和几何意义,以及运算能力.
解:设Z1,Z3对应的复数分别为z1,z3,依题设得z1=
z2[cos(-
)+isin(-
)]=
(1+
i)(
-
i)=
+
iz3=
z2(cos
+isin
)
=
(1+
i)(
+
i)=
+
i
解:设Z1,Z3对应的复数分别为z1,z3,依题设得z1=
| 1 | ||
|
| π |
| 4 |
| π |
| 4 |
| 1 | ||
|
| 3 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 | ||
|
| π |
| 4 |
| π |
| 4 |
=
| 1 | ||
|
| 3 |
| ||
| 2 |
| ||
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:采取合适的复数表达形式可给计算带来很大方便.

练习册系列答案
相关题目
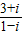 ,-2+i,0,则第四个顶点对应的复数为 .
,-2+i,0,则第四个顶点对应的复数为 .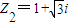 .求Z1和Z3对应的复数.
.求Z1和Z3对应的复数.