题目内容
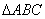 中,
中,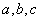 分别是角
分别是角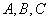 的对边,
的对边,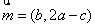 ,
,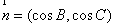 ,且
,且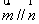
(1)求角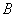 的大小;
的大小;
(2)设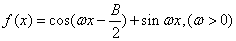 ,且
,且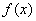 的最小正周期为
的最小正周期为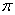 ,求
,求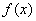 在
在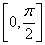 上的最大值和最小值,及相应的
上的最大值和最小值,及相应的 的值。
的值。
【答案】
(1)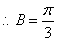
(2)x=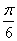 时,f(x)取得最大值
时,f(x)取得最大值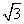 ;x=
;x=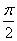 时,f(x)取得最小值-
时,f(x)取得最小值-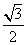 .
.
【解析】
试题分析:(1)由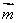 ∥
∥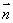 得
得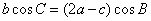 ,
,
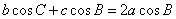
得到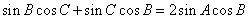 ,
,
所以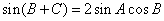 ,又
,又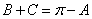 ,所以
,所以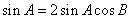
又 ,又
,又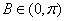 ,
,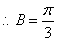
(2) (2)由题知f(x)=cos(ωx-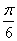 )+sinωx
)+sinωx
=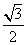 cosωx+
cosωx+ sinωx=
sinωx=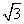 sin(ωx+
sin(ωx+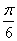 ),
),
由已知得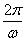 =π,∴ω=2,f(x)=
=π,∴ω=2,f(x)=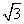 sin(2x+
sin(2x+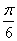 ),
),
当x∈[0,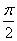 ]时,(2x+
]时,(2x+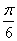 )∈[
)∈[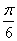 ,
,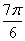 ],
],
sin(2x+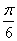 )∈[-
)∈[-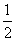 ,1].
,1].
因此,当2x+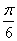 =
= ,即x=
,即x=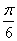 时,f(x)取得最大值
时,f(x)取得最大值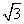 .
.
当2x+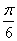 =
=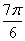 ,即x=
,即x=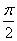 时,f(x)取得最小值-
时,f(x)取得最小值-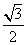 .
.
考点:向量共线,三角函数的性质
点评:主要是考查了三角函数的性质以及解三角形中正弦定理的运用,属于中档题。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
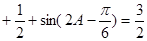 ,
,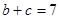 ,
, ,求边
,求边 的长.
的长. ,其中向量
,其中向量
 ,
,
 .
. 的最小正周期;
的最小正周期; 中,
中, 分别是角
分别是角 的对边,
的对边, ,
,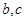 的长.
的长.