题目内容
已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求实数![]() 的值;
的值;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数![]() 的取值范围。
的取值范围。
(3)证明:对任意的正整数![]() ,不等式
,不等式![]() 都成立。
都成立。
(1)a=1 (2) ![]() (3)见解析
(3)见解析
解析:
(1)![]() ………………2分
………………2分
![]() ………………4分
………………4分
(2)由![]() 知
知![]() 由
由![]() 得
得![]() 令
令![]() ,则
,则![]() 在
在![]() 上恰有两个不同的实数根等价于
上恰有两个不同的实数根等价于![]() 在
在![]() 上恰有两个不同的实数根。
上恰有两个不同的实数根。
![]() , ………………6分
, ………………6分
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递减。
上单调递减。
依题意有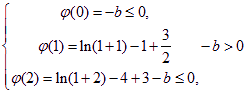
![]() ………………8分
………………8分
(3)![]() 的定义域为
的定义域为![]() ,由
,由![]() 知
知![]() ,令
,令![]() ,得
,得![]() 或
或![]() (舍去),
(舍去),![]() 当
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,![]() 为
为![]() 在
在![]() 上的最大值。
上的最大值。
![]() ,故
,故![]() (当且仅当
(当且仅当![]() 时,等号成立)。
时,等号成立)。
对任意正整数![]() ,取
,取![]() 得
得![]() ,故
,故![]() ………………12分
………………12分

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 在
在 处取得极值.
处取得极值. ;
; ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围. =
= 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 在
在 处取得极值。
处取得极值。 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 为实数。
为实数。 在
在 处取得极值,求
处取得极值,求 的值;
的值;
 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。 在
在 处取得极值.
处取得极值. 的值;[来源:学+科+网]
的值;[来源:学+科+网] 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数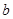 的取值范围.
的取值范围.