题目内容
如图甲,已知PA垂直于⊙O所在平面,AB是⊙O的直径,点C为圆周上异于A、B的一点.
(1)若一个 面体中有
面体中有 个面是直角三角形,则称这个
个面是直角三角形,则称这个 面体的直度为
面体的直度为 .那么四面体
.那么四面体 的直度为多少?说明理由;
的直度为多少?说明理由;
 (2)在四面体
(2)在四面体 中,
中, ,设
,设 .若动点
.若动点 在四面体
在四面体 表面上运动,并且总保持
表面上运动,并且总保持 .设
.设 为动点
为动点 的轨迹围成的封闭图形的面积关于角
的轨迹围成的封闭图形的面积关于角 的函数,求
的函数,求 取最大值时,二面角
取最大值时,二面角 的正切值.
的正切值.
【答案】
解:(1)四面体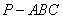 的直度为1.
的直度为1.
 理由如下:由AB是⊙O的直径,点C为圆周上异于A、B的一点,故AC⊥BC, 从而底面为
理由如下:由AB是⊙O的直径,点C为圆周上异于A、B的一点,故AC⊥BC, 从而底面为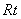 △。又PA垂直于⊙O所在平面,有PA⊥AB,PA⊥AC,故△PAB、△PAC都为
△。又PA垂直于⊙O所在平面,有PA⊥AB,PA⊥AC,故△PAB、△PAC都为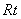 △。又AC为PC在面ABC内的射影,由三垂线定理知PC⊥BC,故△PCB为
△。又AC为PC在面ABC内的射影,由三垂线定理知PC⊥BC,故△PCB为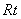 △。综上知四面体
△。综上知四面体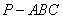 的四个面都为
的四个面都为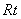 △,所以四面体
△,所以四面体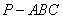 的直度为1. -----------------4分
的直度为1. -----------------4分
(2)∵动点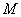 在四面体
在四面体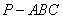 表面上运动,并且总保持
表面上运动,并且总保持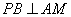 ,
,
∴动点 的轨迹是过点A作PB的垂面与四面体
的轨迹是过点A作PB的垂面与四面体 表面的交线围成的三角形。
表面的交线围成的三角形。
如图乙:平面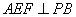 ,并且平面
,并且平面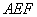 与四面体
与四面体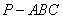 的三个侧面分别交于AE、AF、EF.
的三个侧面分别交于AE、AF、EF.
易知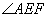 即为二面角
即为二面角 的平面角.
的平面角.
∵AB是⊙O的直径,点C为圆周上异于A、B的一点,∴BC⊥AC
∵PA⊥面ABC,BC 平面ABC,∴BC⊥PA,故BC⊥面PAC,∵AF
平面ABC,∴BC⊥PA,故BC⊥面PAC,∵AF 平面PAC,∴AF⊥BC.
平面PAC,∴AF⊥BC.
又平面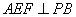 知AF⊥PB,∴AF⊥面PBC.又EF
知AF⊥PB,∴AF⊥面PBC.又EF 平面PBC,AF⊥FE,则
平面PBC,AF⊥FE,则 为
为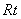 △.
△.
在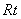 △PAB中,
△PAB中,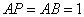 ,
, ,则AE=
,则AE=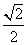 .
.
在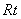 △ACB中,
△ACB中,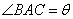 ,
, ,有
,有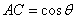 .
.
又在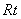 △PAC中,
△PAC中,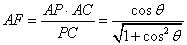 .
.
在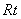
 中,
中,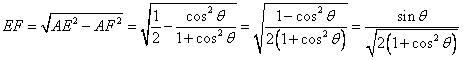 .
.
∴ =
=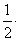


=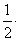

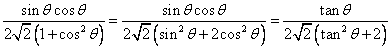

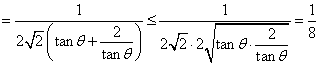 .
.
当且仅当 时
时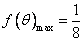 .
.
此时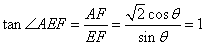 .
.
故 取最大值时二面角
取最大值时二面角 的正切值为1.------------12分
的正切值为1.------------12分

练习册系列答案
相关题目