题目内容
求直线θ=
(ρ∈R)与曲线ρ=
的交点的极坐标.
| π |
| 3 |
| 4 |
| 1-cosθ |
分析:利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,将极坐标方程化成直角坐标方程,在直角坐标系中算出交点的坐标,再利用直角坐标与极坐标间的关系求出其极坐标即可.
解答:解:直线θ=
(ρ∈R)与曲线ρ=
的直角坐标方程分别为y=
x,y2=8x+16,
消元可得,交点坐标为(4,4
),(-
,-
),
化为极坐标为(8,
)和(
,
π).
故答案为:(8,
)和(
,
π).
| π |
| 3 |
| 4 |
| 1-cosθ |
| 3 |
消元可得,交点坐标为(4,4
| 3 |
| 4 |
| 3 |
4
| ||
| 3 |
化为极坐标为(8,
| π |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
故答案为:(8,
| π |
| 3 |
| 8 |
| 3 |
| 4 |
| 3 |
点评:本题考查点的极坐标和直角坐标的互化,考查求交点坐标,解题的关键是掌握极坐标和直角坐标的互化方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
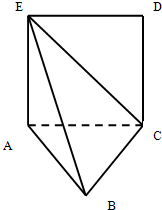 如图,正方形ACDE边长为1且所在的平面与平面ABC垂直,AC⊥BC,且AC=BC.
如图,正方形ACDE边长为1且所在的平面与平面ABC垂直,AC⊥BC,且AC=BC.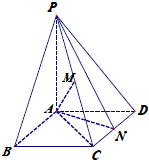 如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.
如图,在菱形ABCD中,∠BAD=120°,点N为CD中点,PA⊥平面ABCD.