Question

若函数f(x)＝(1－x2)(x2＋ax＋b)的图象关于直线x＝－2对称，则f(x)的最大值是________．

 

Answer 1

16

【解析】由题意知

即解得a＝8，b＝15，

所以f(x)＝(1－x2)(x2＋8x＋15)，

则f′(x)＝－4(x＋2)(x2＋4x－1)．

令f′(x)＝0，得x＝－2或x＝－2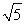－或x＝－2＋，

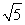当x<－2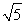－时，f′(x)>0；

当－2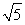－<x<－2时，f′(x)<0；

当－2<x<－2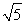＋时，f′(x)>0；

当x>－2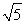＋时，f′(x)<0，

所以当x＝－2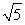－时，f(x)极大值＝16；

当x＝－2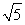＋时，f(x)极大值＝16，所以函数f(x)的最大值为16.