题目内容
4.数列{an}的前n项和Sn ,已知a1=$\frac{1}{2}$,Sn=n2an-n(n-1)(n∈N*),(1)求a2与a3;
(2)求证:数列{$\frac{(n+1){S}_{n}}{n}$}是等差数列;
(3)设bn=$\frac{1}{{S}_{n}{S}_{n+1}}$,数列{an}的前n项和Sn ,证明:Tn$<\frac{5}{2}$(n∈N*).
分析 (1)由a1=$\frac{1}{2}$,Sn=n2an-n(n-1)(n∈N*),分别令n=2,3即可解出;
(2)将an用Sn-Sn-1代换,经过化简整理可得数列{$\frac{(n+1){S}_{n}}{n}$}是等差数列;
(3)Sn=$\frac{{n}^{2}}{n+1}$,可得bn=$\frac{1}{{S}_{n}{S}_{n+1}}$=$\frac{n+2}{{n}^{2}(n+1)}$,当n≥2时,bn<$\frac{n+2}{(n-1)n(n+2)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,即可证明.
解答 解:(1)S2=22a2-2=$\frac{1}{2}$+a2,
解得a2=$\frac{5}{6}$;
S3=32a3-3×2=$\frac{1}{2}$+$\frac{5}{6}$+a3,
解得a3=$\frac{11}{12}$;
(2)Sn=n2an-n(n-1)=n2(Sn-Sn-1)-n(n-1)(n≥2),
∴(n2-1)Sn-n2Sn-1=n(n-1)
∴$\frac{n+1}{n}$Sn-$\frac{n}{n-1}$Sn-1=1(n≥2)
∴数列{$\frac{(n+1){S}_{n}}{n}$}是首项为1,公差为1的等差数列;
(3)证明:$\frac{n+1}{n}$Sn=1+n-1=n,
∴Sn=$\frac{{n}^{2}}{n+1}$(n∈N*),
则bn=$\frac{1}{{S}_{n}{S}_{n+1}}$=$\frac{(n+1)(n+2)}{{n}^{2}•(n+1)^{2}}$=$\frac{n+2}{{n}^{2}(n+1)}$,
当n≥2时,bn<$\frac{n+2}{(n-1)n(n+2)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,
∴当n≥2时,Tn<$\frac{3}{2}$+(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+…+($\frac{1}{n-1}$-$\frac{1}{n}$)
=$\frac{5}{2}$-$\frac{1}{n}$<$\frac{5}{2}$,
当n=1时,上式也成立.
∴Tn<$\frac{5}{2}$(n∈N*).
点评 本题考查了递推式的应用、“裂项求和”、“放缩法”,考查了推理能力与计算能力,属于难题.

 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案(Ⅰ)根据以上数据完成以下2×2列联表:
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 10 | 16 | |
| 女 | 6 | 14 | |
| 总计 | 30 |
(Ⅲ)从不喜爱运动的女志愿者中和喜爱运动的女志愿者中各选1人,求其中不喜爱运动的女生甲及喜爱运动的女生乙至少有一人被选取的概率.
参考公式:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(b+c)(a+c)(b+d)}$(其中n=a+b+c+d)
注:Χ2≤2.706,就认为没有充分证据显示“性别与喜爱运动有关”;Χ2>2.706,就有90%的把握认为“性别与喜爱运动有关”;Χ2>3.841,就有95%的把握认为“性别与喜爱运动有关”.
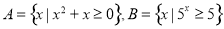 ,则
,则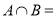 ( )
( )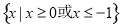 B.
B.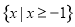
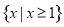 D.
D.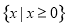
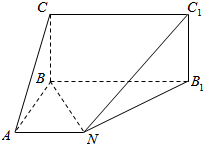 如图:已知矩形BB1C1C所在平面与底面ABB1N垂直,直角梯形ABB1N中AN∥BB1,AB⊥AN,CB=BA=AN=2,BB1=4.
如图:已知矩形BB1C1C所在平面与底面ABB1N垂直,直角梯形ABB1N中AN∥BB1,AB⊥AN,CB=BA=AN=2,BB1=4.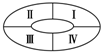 中央电视台“星光大道”节目的现场观众来自4所学校,分别在图中的四个区域Ⅰ,Ⅱ,Ⅲ,Ⅳ坐定.有4种不同颜色的服装,同一学校的观众必须穿上同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否不受限制,那么不同着装方法有多少种?
中央电视台“星光大道”节目的现场观众来自4所学校,分别在图中的四个区域Ⅰ,Ⅱ,Ⅲ,Ⅳ坐定.有4种不同颜色的服装,同一学校的观众必须穿上同种颜色的服装,且相邻两个区域的颜色不同,不相邻区域颜色相同与否不受限制,那么不同着装方法有多少种?