题目内容
13.已知函数f(x)=ax2-blnx在点(1,f(1))处的切线为y=1.(Ⅰ)求实数a,b的值;
(Ⅱ)当x∈(0,1)时,求证:f(x)>x2-x+1
(Ⅲ)若0<x1<x2,求证:$\frac{{x}_{2}-{x}_{1}}{ln{x}_{2}-ln{x}_{1}}$<2x2.
分析 (Ⅰ)求出函数f(x)的导数,由题意可得f(1)=1,f′(1)=0,解方程可得a,b;
( II)令g(x)=f(x)-x2+x-1,求得导数,判断单调性,即可得证;
( III)方法一、由( II)的单调性,可得x∈(0,1)时,x-1>2lnx,由0<x1<x2,可得$0<\frac{x_1}{x_2}<1$,即可得证;
方法二、设φ(x)=2x2(lnx2-lnx)-x2+x,(0<x<x2),求出导数,判断单调性,再由不等式的性质,即可得证.
解答 解:(Ⅰ) $f'(x)=2ax-\frac{b}{x},(x>0)$,
依题意可得$\left\{\begin{array}{l}f(1)=a=1\\ f'(1)=2a-b=0\end{array}\right.$,
解得a=1,b=2;
( II)∵g(x)=f(x)-x2+x-1
=(x-1)-2lnx,x∈(0,1),
∴$g'(x)=1-\frac{2}{x}=\frac{x-2}{x}$,
∵0<x<1,∴g′(x)<0,
∴g(x)在(0,1)上单调递减,
∴g(x)>g(1)=0.即f(x)>x2-x+1;
( III)解法一:由( II)知,x∈(0,1)时,x-1>2lnx.
∵0<x1<x2,∴$0<\frac{x_1}{x_2}<1$,
∴$\frac{x_1}{x_2}-1>2ln\frac{x_1}{x_2}$,∴$\frac{{{x_1}-{x_2}}}{x_2}>2(ln{x_1}-ln{x_2})$,
∵lnx2>lnx1,
∴$\frac{{{x_2}-{x_1}}}{{ln{x_2}-ln{x_1}}}<2{x_2}$.
解法二:设φ(x)=2x2(lnx2-lnx)-x2+x,(0<x<x2)
$φ'(x)=-\frac{{2{x_2}}}{x}+1=\frac{{x-2{x_2}}}{x}$.
当x∈(0,x2),φ′(x)<0,
∴φ(x)在(0,x2)上单调递减
∴φ(x)>φ(x2)=0,
∴x∈(0,x2)时,2x2(lnx2-lnx)>x2-x,
∵0<x1<x2,∴2x2(lnx2-lnx1)>x2-x1,
∵lnx2>lnx1,
∴$\frac{{{x_2}-{x_1}}}{{ln{x_2}-ln{x_1}}}<2{x_2}$.
点评 本题考查导数的运用:求切线方程和单调区间,主要考查函数的单调性的运用,同时考查不等式的性质和运用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 1或4 | B. | 1或2 | C. | 2或4 | D. | 1或5 |
| A. | ∅ | B. | {3} | C. | {0} | D. | {-2} |
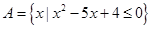 ,集合
,集合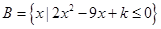 .
.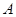 ;
;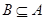 ,求实数
,求实数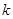 的取值范围.
的取值范围.