Question

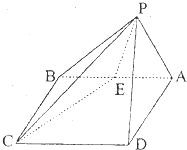如图在四棱锥P-ABCD中，侧面PAD是边长为a的正三角形，二面角P-AD-B为直二面角，ABCD是矩形，E是AB中点，PC与底面ABCD成30°角．
（Ⅰ）求二面角P-EC-D的大小；
（Ⅱ）求D点到平面PEC的距离．

Answer 1

分析：（Ⅰ）取AD中点F，连PF，根据勾股定理可知FE⊥EC，根据二面角平面角的定义可知∠PEF就是其所求二面角的平面角在直角三角形PEF中求出此角即可求得二面角P-EC-D的大小；
（Ⅱ）设D点到平面的距离为h，然后利用等体积法V_D-PCE=V_P-CDE建立关系式解之即可．

解答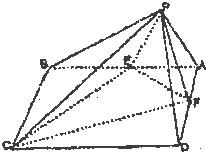：解：（Ⅰ）取AD中点F，连PF，
则PF=

3

2

a且PF⊥平面ABCD，
连CF，则∠PCF=30°
∴CF=

3

2

a，∴CD=

2

a（4分）
∴CE=

6

2

a，连FE，则FE=

3

2

a．
∴FE²+CE²=CF²
∴FE⊥EC，
∴∠PEF就是其所求二面角的平面角（6分）
在Rt△PFE中，∵PF=FE=

3

2

a，∴∠PEF=45°
即二面角P-EC-D的大小为45°（8分）
（Ⅱ）设D点到平面的距离为h，
∵V_D-PCE=V_P-CDE
∴

1

3

•h•

1

2

(

6

2

a)2=

1

3

•

1

2

•

2

a•a•

3

2

a?h=

6

3

a（12分）

点评：本题主要考查了点到平面的距离，以及二面角大小的度量，同时考查了推理能力和计算能力，转化与划归的思想，属于中档题．