题目内容
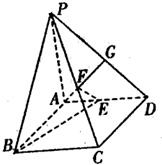
 如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )
如图在四棱锥P-ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点;PA=kAB(k>0),且二面角E-BD-C的平面角大于30°,则k的取值范围是( )分析:建立如图所示空间直角坐标系,设AB的长为1,算出
、
的坐标.利用垂直向量数量积为零的方法,建立方程组解出
=(2,1,-
)是平面EDB的一个法向量且平面CDB的一个法向量为
=(0,0,1),算出<
,
>的余弦之值,结合题意建立关于k的不等式,解之即可得到实数k的取值范围.
| BD |
| BE |
| n |
| 2 |
| k |
| m |
| m |
| n |
解答:解:以A为原点,以AB、AD、AP为x轴、y轴、z轴,建立空间直角坐标系如图所示,
设AB的长为1,则
=(-1,2,0),
=(0,1,
)
平面CDB的一个法向量为
=(0,0,1),
设平面EDB的一个法向量为
=(x,y,z),
则
,取y=1,可得
=(2,1,-
),
设二面角E-BD-C的大小为θ,
则cosθ=|cos<
,
>|═
<
化简得k2>
,所以k>
.

设AB的长为1,则
| BD |
| BE |
| k |
| 2 |
平面CDB的一个法向量为
| m |
设平面EDB的一个法向量为
| n |
则
|
| n |
| 2 |
| k |
设二面角E-BD-C的大小为θ,
则cosθ=|cos<
| m |
| n |
| ||||
|
| ||
| 2 |
化简得k2>
| 4 |
| 15 |
2
| ||
| 15 |
点评:本题给出二面角的平面角的范围,求实数k的范围.着重考查了空间向量的夹角公式和利用空间直角坐标系研究平面与平面所成角等知识,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2
如图在四棱锥P-ABCD中,底ABCD是矩形,PA⊥面ABCD,AP=AB=2,BC=2 如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点
如图在四棱锥P-ABCD中侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD为直角梯形.其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点 如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形,
如图在四棱锥P-ABCD中,侧棱PD⊥平面ABCD,M,N分别是AB,PC的中点,底面ABCD是菱形, 如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.
如图在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,垂足为点A,PA=AB=1,点M,N分别是PD,PB的中点.