题目内容
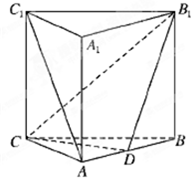 如图所示,在正三棱柱ABC-A1B1C1中,AB=AC=BC=BB1=2,D点为棱AB的中点.
如图所示,在正三棱柱ABC-A1B1C1中,AB=AC=BC=BB1=2,D点为棱AB的中点.(1)求证:AC1∥平面CDB1
(2)求BB1与平面CDB1所成角的正切值.
分析:(1)证明线面平行,只需证明AC1平行于平面CDB1内的一条直线,利用三角形的中位线可证;
(2)先证明平面CDB1⊥ABB1A1,过B作BE⊥B1D,则∠BB1E是BB1与平面CDB1所成角,从而可求BB1与平面CDB1所成角的正切值.
(2)先证明平面CDB1⊥ABB1A1,过B作BE⊥B1D,则∠BB1E是BB1与平面CDB1所成角,从而可求BB1与平面CDB1所成角的正切值.
解答: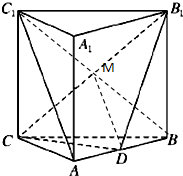 (1)证明:连接BC1交B1C于M,连接DM
(1)证明:连接BC1交B1C于M,连接DM
∴M是B1C的中点
∵D是AB的中点,∴MD∥AC1,
又MD?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(2)解:∵正三棱柱ABC-A1B1C1中,D点为棱AB的中点.
∴CD⊥平面ABB1A1,
∵CD?平面CDB1.
∴平面CDB1⊥ABB1A1,
过B作BE⊥B1D,∵平面CDB1∩ABB1A1=B1D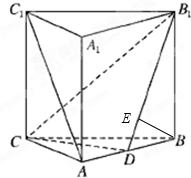
∴BE⊥平面CDB1.
∴∠BB1E是BB1与平面CDB1所成角
∵BB1⊥BD
∴△BEB1∽△DBB1,
由BD=
AB=1,BB1=2得tan∠BB1E=
即BB1与平面CDB1所成角的正切值为
 (1)证明:连接BC1交B1C于M,连接DM
(1)证明:连接BC1交B1C于M,连接DM∴M是B1C的中点
∵D是AB的中点,∴MD∥AC1,
又MD?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.
(2)解:∵正三棱柱ABC-A1B1C1中,D点为棱AB的中点.
∴CD⊥平面ABB1A1,
∵CD?平面CDB1.
∴平面CDB1⊥ABB1A1,
过B作BE⊥B1D,∵平面CDB1∩ABB1A1=B1D

∴BE⊥平面CDB1.
∴∠BB1E是BB1与平面CDB1所成角
∵BB1⊥BD
∴△BEB1∽△DBB1,
由BD=
| 1 |
| 2 |
| 1 |
| 2 |
即BB1与平面CDB1所成角的正切值为
| 1 |
| 2 |
点评:本题重点考查线面平行,考查线面角,解题的关键是正确运用线面平行的判断,正确找出线面角,综合性强.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
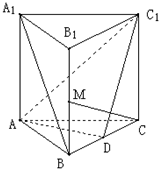 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,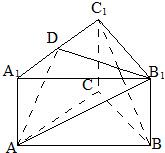 如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为
如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为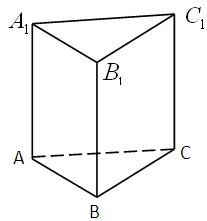
 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM=
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM= (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.