题目内容
如图所示,在正三棱柱ABC-A1B1C1中,所有棱长均为1,求点B1到平面ABC1的距离.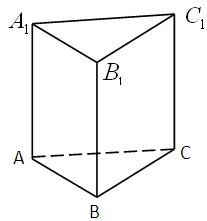
分析:点到面的距离计算通常采用等体积法,由图,B1到平面ABC1的距离即棱锥VB1-ABC1的高,而其体积与VC1-ABB1,VC1-ABB1易求,由此知只须解出面A1B1C1的面积即可.
解答: 解:由题意及图可知,S△ABB1=
解:由题意及图可知,S△ABB1=
,C1到面ABB1的距离是
故VC1-ABB1=
×
×
=
由正三棱柱的结构特征,C1到线AB的距离是
=
故 S△ABC1=
×1×
=
令B1到平面ABC1的距离为h,
由VB1-ABC1=VC1-ABB1
故
×h×
=
解得h=
即B1到平面ABC1的距离为
.
 解:由题意及图可知,S△ABB1=
解:由题意及图可知,S△ABB1=| 1 |
| 2 |
| ||
| 2 |
故VC1-ABB1=
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 12 |
由正三棱柱的结构特征,C1到线AB的距离是
12+ (
|
| ||
| 2 |
故 S△ABC1=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
令B1到平面ABC1的距离为h,
由VB1-ABC1=VC1-ABB1
故
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
解得h=
| ||
| 7 |
即B1到平面ABC1的距离为
| ||
| 7 |
点评:本题的考点是点、线、面间的距离计算,根据几何体的结构灵活选择求解方法,点到面的距离计算常采用的方法是等体积法,其特征是一个几何体积有多个角度来求体积,且其中有一个易求,而点所对的面的面积易求,如此,则适合用等体积法求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
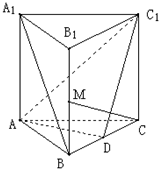 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,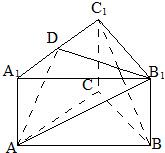 如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为
如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM=
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM= (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.