题目内容
13.函数f(x)=$\frac{sinx}{sinx+cosx}$在区间[0,$\frac{π}{2}$]上的最大值与最小值分别是 ( )| A. | 1,0 | B. | $\frac{1}{2}$,0 | C. | 0,-1 | D. | 1,$\frac{1}{2}$ |
分析 求出x=0和x=$\frac{π}{2}$时的值,然后分子分母同时除以cosx,转化为含有正切的函数,由tanx在(0,$\frac{π}{2}$)上的范围求得答案.
解答 解:当x=0时,f(x)=$\frac{sinx}{sinx+cosx}$=0;
当x=$\frac{π}{2}$时,f(x)=$\frac{sinx}{sinx+cosx}$=1;
当x≠0且x$≠\frac{π}{2}$时,f(x)=$\frac{sinx}{sinx+cosx}$=$\frac{tanx}{tanx+1}$=$\frac{1}{1+\frac{1}{tanx}}$.
∵x∈(0,$\frac{π}{2}$),∴tanx∈(0,+∞),
则$\frac{1}{tanx}∈$(0,+∞),1+$\frac{1}{tanx}∈$(1,+∞),
∴$\frac{1}{1+\frac{1}{tanx}}∈$(0,1).
综上,f(x)∈[0,1].
故选:A.
点评 本题考查三角函数的最值的求法,体现了分类讨论的数学思想方法,注意极限思想的运用,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.设函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x+1}-\frac{1}{2},x≥1}\\{1,x<1}\end{array}\right.$,则不等式f(6-x2)>f(x)的解集为( )
| A. | (-3,1) | B. | (-3,2) | C. | (-2,$\sqrt{5}$) | D. | (-$\sqrt{5}$,2) |
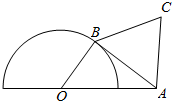 如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.
如图所示,半圆O的直径为2,A为半圆直径的延长线上的一点,且OA=2,B为半圆上任一点,以AB为边向右上方作等边△ABC.