Question

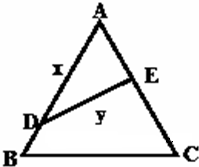有一展馆形状是边长为2的等边三角形ABC，DE把展馆分成上下两部分面积比为1：2（如图所示），其中D在AB上，E在AC上．
（1）若D是AB中点，求AE的值；
（2）设AD=x，ED=y．（ⅰ）求用x表示y的函数关系式；（ⅱ）若DE是消防水管，为节约成本，希望它最短，DE的位置应在哪里？若DE是参观线路，则希望它最长，DE的位置又应在哪里？请给以说明．

Answer 1

分析：（1）根据题意可得S△ADE=

1

3

S△ABC，再由△ABC是等边三角形且D是AB中点，利用三角形的面积公式建立关于AD、AE的等式，解之可得AE=

4

3

；
（2）（i）在△ADE中，根据余弦定理建立y²关于x²的等式，两边开方可得用x表示y的函数关系式，再由AE≤2算出

2

3

≤x≤2，可得此函数的定义域；
（ⅱ）若DE是消防水管，则根据基本不等式加以计算，可得当AE=

2 3

3

时消防水管路线最短为

2 3

3

；若DE是参观线路，利用函数的单调性的定义加以证明，可得函数y=

x2+ 16 9x2 - 4 3

在区间[

2

3

，

2

3

3

]上为减函数，在区间[

2

3

3

，2]上为增函数，由此可得当x=

2

3

或x=2时DE最长，进而得到此时D、E两点的位置．

解答：解：（1）根据题意，可得S△ADE=

1

3

S△ABC=

1

3

•

1

2

•22•sin60°=

3

3

，
∵S△ADE=

1

2

AD•AE•sin60°，∴AD•AE=

4

3

，
又∵D是AB中点，可得AD=1，
∴AD•AE=AE=

4

3

，即AE的值为

4

3

；
（2）∵AD•AE=

4

3

，∴AE=

4

3AD

=

4

3x

，
又∵AE≤2，∴0＜

4

3x

≤2，解得x≥

2

3

，可得

2

3

≤x≤2．
△ADE中，根据余弦定理，
可得y2=DE2=AD2+AE2-2AD•AE•cos60°=x2+

16

9x2

-

4

3

∴y=

x2+ 16 9x2 - 4 3

，x∈[

2

3

，2]
①若DE是消防水管，则y=

x2+ 16 9x2 - 4 3

≥

2• x2• 16 9x2 - 4 3

=

2 3

3

，
当且仅当x2=

4

3

，即x=

2 3

3

，等号成立．
此时AE=

2 3

3

，故DE∥BC，且消防水管路线最短为DE=

2 3

3

；
②若DE是参观线路，令x2=t，t∈[

4

9

，4]，y=

t+ 16 9t - 4 3

，设f(t)=t+

16

9t

，
可以证明f（t）在[

4

9

，

4

3

]是减函数：
设

4

9

≤t1＜t2≤

4

3

，则f(t1)-f(t2)=(t1-t2)+

16

9

(

1

t1

-

1

t2

)=(t1-t2)•

(t1t2- 16 9 )

t1t2

，
∵

4

9

≤t1＜t2≤

4

3

，可得t1-t2＜0，t1t2＜

16

9

，
∴f（t₁）-f（t₂）＞0，得f（t₁）＞f（t₂），
∴f（t）在[

4

9

，

4

3

]是减函数，同理可证f（t）在[

4

3

，4]是增函数．
因此，f（t）的最大值为f(

4

9

)、f(4)二者中较大的值，
∵f(

4

9

)=f(4)=

40

9

，∴ymax=

40 9 - 4 3

=

2 7

3

，
此时x=

2

3

或x=2．当x=

2

3

时，AE=2；当x=2时，AE=

2

3

．
综上所述，当D为AB的靠近A的一个三等分点且E与C重合；或E为靠近A的AC的一个三等分点且D与B重合时，
参观线路DE最长，最长路线为

2 7

3

．

点评：本题给出实际应用问题，求消防水管路线的最小值与参观路线的最大值．着重考查了利用正余弦定理解三角形、函数的单调性及其应用、利用基本不等式求最值和三角函数在实际问题中的应用等知识，属于中档题．