题目内容
1．棱长为4的正方体ABCD-A1B1C1D1中，P，Q是CC1上两动点，且PQ=1，则三棱锥P-AQD的体积为（ ）| A． | 8 | B． | $\frac{16}{3}$ | C． | 3 | D． | $\frac{8}{3}$ |
分析 将三角形PDQ看做棱锥的底面，将A当做棱锥的顶点，则底面三角形一边为PQ，此边上的高是4，棱锥的高为4，代入体积公式计算．
解答 解：S△PDQ=$\frac{1}{2}$×PQ×CD=2，
∵AD⊥平面PDQ，
∴AD为棱锥A-PDQ的高，
∴V棱锥P-AQD=V棱锥A-PDQ=$\frac{1}{3}$×S△PDQ×AD=$\frac{1}{3}×2×4$=$\frac{8}{3}$．
故选D．
点评 本题考查了棱锥的体积计算，选取恰当的底面可使计算简化，是求体积中常用的一种方法．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
9．
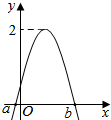如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）
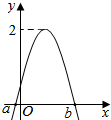如图是函数$f（x）=Asin（2x+ϕ），（A＞0，|ϕ|≤\frac{π}{2}）$图象的一部分，对不同的x1，x2∈[a，b]，若f（x1）=f（x2），有$f（{x_1}+{x_2}）=\sqrt{2}$，则（ ）| A． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是增函数 | B． | f（x）在$（-\frac{3π}{8}，\frac{π}{8}）$上是减函数 | ||
| C． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是增函数 | D． | f（x）在$（-\frac{5π}{12}，\frac{π}{12}）$上是减函数 |
10．函数f（x）=ax2+bx-2是定义在[1+a，2]上的偶函数，则f（x）在区间[-1，2]上的值域是（ ）
| A． | [-10，2] | B． | [-14，-2] | C． | （-∞，-2] | D． | [-14，-5] |
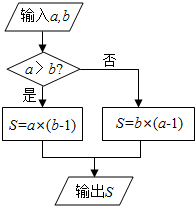
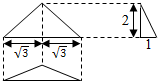已知一个三棱锥的三视图如图所示，则该三棱锥的体积为$\frac{2\sqrt{3}}{3}$．外接球半径为$\sqrt{5}$．