题目内容
(2012•芜湖二模)直线
(t为参数)被曲线ρ=
cos(θ+
)所截的弦长为( )
|
| 2 |
| π |
| 4 |
分析:先把参数方程和极坐标方程化为普通方程,并求出圆心到直线的距离d,再利用关系:l=2
即可求出弦长l.
| r2-d2 |
解答:解:直线
(t为参数)化为普通方程:直线3x+4y+1=0.
∵曲线ρ=
cos(θ+
),展开为ρ=cosθ-sinθ,∴ρ2=ρcosθ-ρsinθ,化为普通方程为x2+y2=x-y,即(x-
)2+(y+
)2=
,
∴圆心C(
,-
),r=
.
圆心C到直线距离d=
=
,
∴直线被圆所截的弦长=2
=
.
故选C.
|
∵曲线ρ=
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴圆心C(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
圆心C到直线距离d=
|3×
| ||||
|
| 1 |
| 10 |
∴直线被圆所截的弦长=2
| r2-d2 |
| 7 |
| 5 |
故选C.
点评:正确运用弦长l、圆心到直线的距离、半径r三者的关系:l=2
是解题的关键.
| r2-d2 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
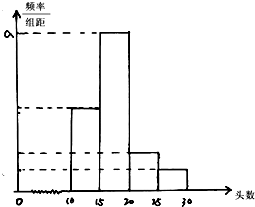 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: