题目内容
(2012•芜湖二模)将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有5种颜色可供使用,则不同的染色方法总数有( )
分析:首先给顶点P选色,有5种结果,再给A选色有4种结果,再给B选色有3种结果,最后分两种情况即C与B同色与C与B不同色来讨论,根据分步计数原理和分类计数原理得到结果.
解答:解:四棱锥为P-ABCD.下面分两种情况即C与B同色与C与B不同色来讨论,
(1)各个点的不同的染色方法 P:C51,A:C41,B:C31,C与B同色:1,D:C31 ,故共有
•C41•C31•C31 种.
(2)各个点的不同的染色方法 P:C51,A:C41,B:C31,C与B不同色C21,D:C21,故共有
•C41•C31•C21•C21 种
由分步计数原理可得不同的染色方法总数有
•C41•C31•C31 +
•C41•C31•C21•C21 =420.
故选D.
(1)各个点的不同的染色方法 P:C51,A:C41,B:C31,C与B同色:1,D:C31 ,故共有
| C | 1 5 |
(2)各个点的不同的染色方法 P:C51,A:C41,B:C31,C与B不同色C21,D:C21,故共有
| C | 1 5 |
由分步计数原理可得不同的染色方法总数有
| C | 1 5 |
| C | 1 5 |
故选D.
点评:本题主要排列与组合及两个基本原理,总结此类问题的做法,对于复杂一点的计数问题,有时分类以后,每类方法并不都是一步完成的,必须在分类后又分步,综合利用两个原理解决,属于中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
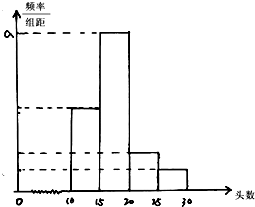 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: