题目内容
【题目】如图，四边形
是边长为
的正方形，
为
的中点，以
为折痕把
折起，使点
到达点
的位置，且二面角
为直二面角，连结
.
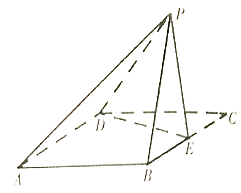
（1）记平面
与平面
相较于
，在图中作出，并说明画法；
（2）求直线与平面
所成角的正弦值.
【答案】（1）详见解析（2）
【解析】
(1)只需延长
交于
点，连结
，即可满足是平面
与平面
的交线；
(2)先作用
交
于
，得到
两两垂直，以点为坐标原点，建立空间直角坐标系，求出平面
的法向量，和直线
的方向向量，由向量的夹角公式结合线面角的范围，即可求出结果.
解：（1）延长交于点，连接，则直线即为.
（2）过
作交于，则
，所以
是二面角
的平面角的补角，因为二面角为直二面角，从而
，即
.
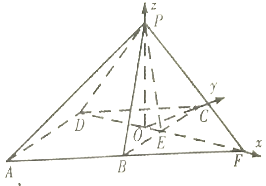
以为坐标原点，分别以
为
轴，
轴，
轴正方向建立空间直角坐标系，如图，在
中，
，
，所以
，从而
，所以
，
，又
，
，则
，
，
，
，
，
所以
，
，
，
设平面的法向量为
，则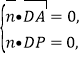
取
，
，
，
，
所以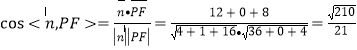
，
设直线与平面所成角为
，则
，
所以直线与平面所成角的正弦值为.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
【题目】某火锅店为了解气温对营业额的影响，随机记录了该店1月份中5天的日营业额y(单位：千元)与该地当日最低气温x(单位：℃)的数据，如下表：
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
（1）求y关于x的回归方程
；
（2）判定y与x之间是正相关还是负相关；若该地1月份某天的最低气温为6℃，用所求回归方程预测该店当日的营业额；
附：①
；
.
②参考数据如下：
i |
|
|
|
|
1 | 2 | 12 | 4 | 24 |
2 | 5 | 10 | 25 | 50 |
3 | 8 | 8 | 64 | 64 |
4 | 9 | 8 | 81 | 72 |
5 | 11 | 7 | 121 | 77 |
| 35 | 45 | 295 | 287 |
【题目】已知椭圆
、抛物线
的焦点均在
轴上，的中心和的顶点均为原点
，从每条曲线上取两个点，将其坐标记录于下表中：
| 3 |
| 4 |
|
|
| 0 |
|
|
（Ⅰ）求
的标准方程；
（Ⅱ）请问是否存在直线
满足条件：①过的焦点
；②与交不同两点
且满足
？若存在，求出直线的方程；若不存在，说明理由．
