题目内容
（本小题满分12分）
（1）判断函数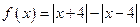
的奇偶性；
（
2）若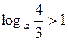
，求a的取值范围.
（1）判断函数
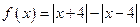的奇偶性；（
2）若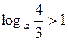，求a的取值范围.解：（1）奇函数．………………………………………………………6分
（2）1<a<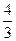
. ……………………………………………………………………………12分
（2）1<a<
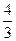. ……………………………………………………………………………12分略
练习册系列答案
相关题目
题目内容
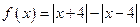的奇偶性；2）若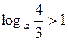，求a的取值范围.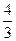. ……………………………………………………………………………12分
的定义域为
（
为实数）.
时，求函数
的值域；
的值.
(x≠0，常数a∈R).
，如果
，则
等于（ ）
是定义在R上的奇函数，其最小正周期为3, 且
时
，则
= （ ）
，B={
}，若B
A，则-3
a
与直线x=l的交点个数为0或l；
，+∞）时，函数
的值域为R；
关于点（1，-1）对称的函数为
（2 -x
）.
,
(
). 
恒成立”的只有（ ） 
在
内单调递减，则不等式
的解集是 ．
家庭5月份的高峰时间段用电量为
千瓦时，低谷时间段用电量为
千瓦时，
费为 元（用数字作答）