题目内容
(本小题满分12分)求函数y=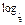 (4x-x2)的单调区间.
(4x-x2)的单调区间.
解:由4x-x2>0,得函数的 定义域是(0,4).令t=4x-x2,则y=
定义域是(0,4).令t=4x-x2,则y=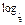 t.
t.
∵t=4x-x2=-(x-2)2+4,∴t=4x-x2 的单调减区间是[2,4],增区间是(0,2).
的单调减区间是[2,4],增区间是(0,2).
又y=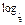 t在(0,+∞)上是减函数,
t在(0,+∞)上是减函数,
∴函数y=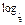 (4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
(4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
解析

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若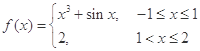 ,则
,则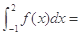 ( )
( )
| A.0 | B.1 | C.2 | D.3 |
函数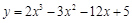 在[0,3]上的最大值和最小值分别是( ).
在[0,3]上的最大值和最小值分别是( ).
| A.5,-15 | B.5,-14 | C.5,-16 | D.5,15 |
 米,记∠BHE=θ.
米,记∠BHE=θ.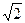 ,求此时管道的长度L;
,求此时管道的长度L;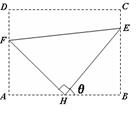
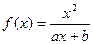 (a,b为常数)且方程f(x)-x+12=0
(a,b为常数)且方程f(x)-x+12=0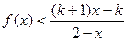 .
.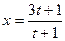 。已知2010年生产饮料的设备折旧
。已知2010年生产饮料的设备折旧 ,维修等固定费用为3 万元,每生产1万件
,维修等固定费用为3 万元,每生产1万件 成本—促销费,生产成本=固定费用+生产费用)
成本—促销费,生产成本=固定费用+生产费用)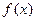 有最小正周期4,且
有最小正周期4,且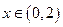 时,
时,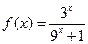 。
。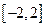 上的解析式;
上的解析式;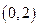 上的单调性,并给予证明;
上的单调性,并给予证明;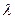 为何值时,关于方程
为何值时,关于方程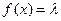 在
在 甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.
甲将经营状态良好的某种消费品专卖店以58万元的优惠价转让给企业乙,约定乙用经营该店的利润偿还转让费(不计息).已知经营该店的固定成本为6.8万元/月,该消费品的进价为16元/件,月销量q(万件)与售价p(元/件)的关系如图.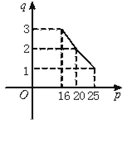
 ,
, ,函数
,函数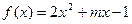
 的解集为C,当
的解集为C,当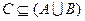 时,求实数
时,求实数 取值范围
取值范围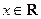 ,都有
,都有 成立,试求
成立,试求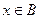 时,
时,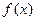 的值
的值 域
域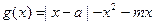
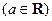 ,求
,求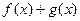 的最小值
的最小值