题目内容
已知函数f(x)满足对任意的x∈R都有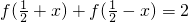 成立,则
成立,则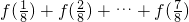 =________.
=________.
7
分析:由题意得两个式子相加可得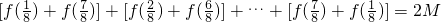 ,因为
,因为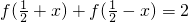 所以
所以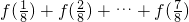 =7
=7
解答:设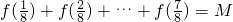 …①
…①
所以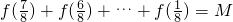 …②
…②
①+②可得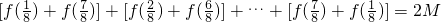
因为函数f(x)满足对任意的x∈R都有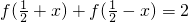 成立
成立
所以14=2M即M=7
所以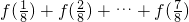 =7
=7
故答案为:7.
点评:本题考查了利用函数的对称性求和,解决本题的关键是发现函数与和式的对称性,利用倒叙相加法求和.此法在数列部分常见,也是一种求和的重要方法.
分析:由题意得两个式子相加可得
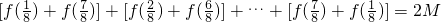 ,因为
,因为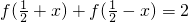 所以
所以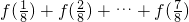 =7
=7解答:设
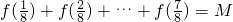 …①
…①所以
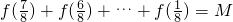 …②
…②①+②可得
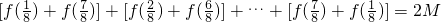
因为函数f(x)满足对任意的x∈R都有
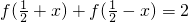 成立
成立所以14=2M即M=7
所以
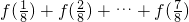 =7
=7故答案为:7.
点评:本题考查了利用函数的对称性求和,解决本题的关键是发现函数与和式的对称性,利用倒叙相加法求和.此法在数列部分常见,也是一种求和的重要方法.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目