题目内容
17.已知椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$的左右焦点为F1、F2,点P为其上动点,点Q(3,2),则|PF1|-|PQ|的最大值为( )| A. | $6-\sqrt{5}$ | B. | $\sqrt{29}-6$ | C. | $6+\sqrt{5}$ | D. | $\sqrt{29}-4$ |
分析 由|PF1|-|PQ|=2a-(|PF2|+|PQ|)≤2a-|QF2|,即可得出.
解答 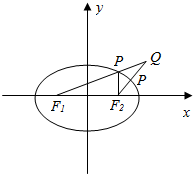 解:如图所示.
解:如图所示.
F1(-2,0),F2(2,0).
|QF2|=$\sqrt{(3-2)^{2}+{2}^{2}}$=$\sqrt{5}$.
由椭圆的定义可得:|PF1|+|PF2|=2a=6.
∴|PF1|-|PQ|=2a-(|PF2|+|PQ|)≤2a-|QF2|=6-$\sqrt{5}$.
故选:A.
点评 本题考查了椭圆的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
5.已知M={x∈N|$\frac{6}{6-x}$∈N},则集合M的子集的个数是( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
9.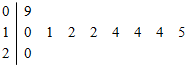 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
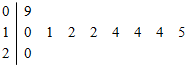 10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )
10名工人某天生产同一零件,生产的件数茎叶图如图所示,若众数为c,则c=( )| A. | 12 | B. | 14 | C. | 15 | D. | 17 |
6.设数列{an}满足a1=0,且2an+1=1+anan+1,bn=$\frac{1}{{\sqrt{n}}}-\sqrt{\frac{{{a_{n+1}}}}{n}}$,记Sn=b1+b2+…+bn,则S100=( )
| A. | $1-\frac{1}{{\sqrt{101}}}$ | B. | $\frac{9}{10}$ | C. | $\frac{99}{100}$ | D. | $\frac{1}{10}-\frac{1}{{\sqrt{101}}}$ |
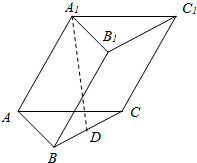 如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.
如图,斜三棱柱ABC-A1B1C1的底面是边长为4的正三角形,D是BC的中点,A1D⊥平面ABC.