题目内容
【题目】已知椭圆的焦点坐标为![]() ,且短轴一顶点
,且短轴一顶点![]() 满足
满足![]() .
.
(1)求椭圆的方程;
(2)过![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)当直线
;(2)当直线![]() ,
,![]() 内切圆面积的最大值为
内切圆面积的最大值为![]()
【解析】
试题分析:(1)设椭圆方程,由焦点坐标可得![]() ,由
,由![]()
可得![]() ,又
,又![]() ,由此可求椭圆方程;
,由此可求椭圆方程;
(2)设![]() ,不妨
,不妨![]() ,设
,设![]() 的内切圆的半径为
的内切圆的半径为![]() ,则
,则![]() 的周长为8,
的周长为8,![]() ,因此
,因此![]() 最大,
最大,![]() 就最大.设直线
就最大.设直线![]() 的方程为
的方程为![]() ,与椭圆方程联立,从而可表示
,与椭圆方程联立,从而可表示![]() 的面积,利用换元法,借助于导数,即可求得结论
的面积,利用换元法,借助于导数,即可求得结论
试题解析:(1)由题,设椭圆方程![]() ,不妨设
,不妨设![]() ,则
,则![]() ,∴
,∴![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
(2)设![]() ,不妨设
,不妨设![]() ,设
,设![]() 的内切圆半径为
的内切圆半径为![]() ,则
,则![]() 的周长为8,面积
的周长为8,面积![]() ,因此
,因此![]() 最大,
最大,![]() 就最大,由题知,直线
就最大,由题知,直线![]() 的斜率不为零,可设直线
的斜率不为零,可设直线![]() 的方程为
的方程为![]() ,由
,由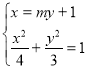 得
得![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,则
,则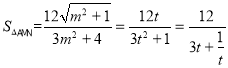 ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,故有
上单调递增,故有![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() ,这时所求内切圆面积的最大值为
,这时所求内切圆面积的最大值为![]() .
.
故直线![]() ,
,![]() 内切圆面积的最大值为
内切圆面积的最大值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】若学生![]() 一天学习数学超过两个小时的概率为
一天学习数学超过两个小时的概率为![]() (每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(每天是相互独立没有影响的),一周内至少有四天每天学习数学超过两个小时,就说该生本周数学学习是投入的.
(Ⅰ)①设学生![]() 本周一天学习数学超过两个小时的天数为
本周一天学习数学超过两个小时的天数为![]() 求
求![]() 的分布列与数学期望
的分布列与数学期望![]()
②求学生![]() 本周数学学习投入的概率.
本周数学学习投入的概率.
(Ⅱ)为了研究学生学习数学的投入程度和本周数学周练成绩的关系,随机在年级中抽取了![]() 名学生进行调查,所得数据如下表所示:
名学生进行调查,所得数据如下表所示:
成绩理想 | 成绩不太理想 | 合计 | |
数学学习投入 | 20 | 10 | 30 |
数学学习不太投入 | 10 | 15 | 25 |
合计 | 30 | 25 | 55 |
根据上述数据能否有![]() 的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
的把握认为“学生学习数学的投入程度和本周数学成绩两事件有关”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |