题目内容
如图甲是某条公共汽车线路收支差额 与乘客量
与乘客量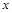 的图象(收支差额=车票收入—支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格.下面给出四个图象:在这些图象中( )
的图象(收支差额=车票收入—支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)是不改变车票价格,减少支出费用;建议(Ⅱ)是不改变支出费用,提高车票价格.下面给出四个图象:在这些图象中( )
| A.①反映了建议(Ⅱ),③反映了建议(Ⅰ) |
| B.①反映了建议(Ⅰ),③反映了建议(Ⅱ) |
| C.②反映了建议(Ⅰ),④反映了建议(Ⅱ) |
| D.④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
B
解析试题分析:直线的斜率说明票价问题;当x=0的点说明公司的成本情况,再结合图象进行说明.根据题意和图①知,两直线平行即票价不变,直线向上平移说明当乘客量为0时,收入是0但是支出的变少了,即说明了此建议是降低成本而保持票价不变;由图③看出,当乘客量为0时,支出不变,但是直线的倾斜角变大,即相同的乘客量时收入变大,即票价提高了,即说明了此建议是提高票价而保持成本不变,
考点:函数图象、数形结合思想。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,既是奇函数又是增函数的为( )
| A.y=x+1 | B.y=-x3 |
C.y= | D.y=x|x| |
x为实数,[x]表示不超过x的最大整数,则函数f(x)=x-[x]在R上为( )
| A.奇函数 | B.偶函数 |
| C.增函数 | D.周期函数 |
设函数f(x)(x∈R)满足f(-x)=f(x),f(x)=f(2-x),且当x∈[0,1]时,f(x)=x3.又函数g(x)=|xcos(πx)|,则函数h(x)=g(x)-f(x)在 上的零点个数为( )
上的零点个数为( )
| A.5 | B.6 | C.7 | D.8 |
已知函数y=f(x)的图象如图,则不等式f(3x-x2)<0的解集为( )
| A.{x|1<x<2} | B.{x|0<x<3} |
| C.{x|x<1或x>2} | D.{x|x<0或x>3} |
设a为实数,函数f(x)=x3+ax2+(a-2)x的导数是f′(x),且f′(x)是偶函数,则曲线y=f(x)在原点处的切线方程为( )
| A.y=-2x | B.y=3x |
| C.y=-3x | D.y=4x |
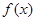 是定义在
是定义在 上的偶函数,
上的偶函数, 为奇函数,
为奇函数, ,当
,当 时,
时, log2x,则在
log2x,则在 内满足方程
内满足方程 的实数
的实数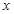 为
为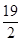



 的图象大致是( )
的图象大致是( )
 对任意x∈R恒成立,则f(2011)等于( )
对任意x∈R恒成立,则f(2011)等于( )