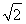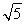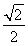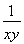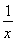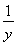题目内容
如图所示,在四棱锥P-ABCD中,△PBC为正三角形,PA⊥底面ABCD,其三视图如图所示,俯视图是直角梯形.


(1)求正视图的面积;
(2)求四棱锥P-ABCD的体积.
(1)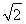 (2)
(2)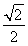
【解析】(1)如图所示,过A作AE∥CD交BC于E,联结PE.根据三视图可知,E是BC的中点,

且BE=CE=1,AE=CD=1,
又∵△PBC为正三角形,
∴BC=PB=PC=2,且PE⊥BC.
∴PE2=PC2-CE2=3.
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE,
∴PA2=PE2-AE2=2,即PA=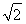 ,
,
∴正视图的面积为S=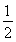 ×2×
×2×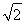 =
=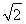 .
.
(2)由(1)可知,四棱锥P-ABCD的高PA=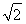 ,
,
底面积为S= ·CD=
·CD=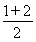 ×1=
×1=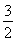
∴四棱锥P-ABCD的体积V四棱锥P-ABCD=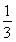 S·PA=
S·PA=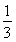 ×
×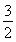 ×
×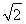 =
=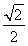 .
.

练习册系列答案
相关题目