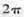题目内容
(.(本小题满分12分)
设某几何体及其三视图:如图(尺寸的长度单位:m)
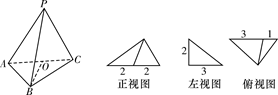
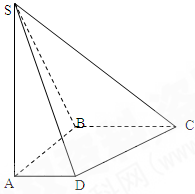
(1)O为AC的中点,证明:BO⊥平面APC;
(2)求该几何体的体积;
(3)求点A到面PBC的距离.
设某几何体及其三视图:如图(尺寸的长度单位:m)

(1)O为AC的中点,证明:BO⊥平面APC;
(2)求该几何体的体积;
(3)求点A到面PBC的距离.
解:(1)证明:由三视图可知,面PAC⊥面ABC,BO⊥AC
∴BO⊥平面APC.(3分)
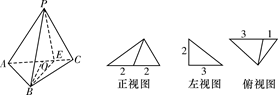
(2)过P点在面PAC内作PE⊥AC交AC于E,由俯视图可知:CE=1,AE=3
又BO=3,AC=4,∴S△ABC=×4×3=6
∴VP-ABC=×6×2=4.(7分)
(3)∵PC==,BE==
∴PB==,BC==
∴cos∠PBC===
=
∴sin∠PBC==
∴S△PBC=PB·BC·sin∠PBC= ··
··
=
设点A到面PBC的距离为h.
∵VA-PBC=VP-ABC,∴h·S△PBC=4
∴h= ==.(12分)
==.(12分)
∴BO⊥平面APC.(3分)

(2)过P点在面PAC内作PE⊥AC交AC于E,由俯视图可知:CE=1,AE=3
又BO=3,AC=4,∴S△ABC=×4×3=6
∴VP-ABC=×6×2=4.(7分)
(3)∵PC==,BE==
∴PB==,BC==
∴cos∠PBC===
=
∴sin∠PBC==
∴S△PBC=PB·BC·sin∠PBC=
 ··
··=
设点A到面PBC的距离为h.
∵VA-PBC=VP-ABC,∴h·S△PBC=4
∴h=
 ==.(12分)
==.(12分)略

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 B 1∶3 C 1∶3
B 1∶3 C 1∶3 BCD中,
BCD中,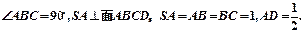
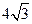 厘米的直三棱柱(直三棱柱指底面为三角形,侧棱与底面垂直的三棱柱)封闭容器内可以向各个方向自由运动,则该小球不可能接触到的容器内壁的面积是:( )
厘米的直三棱柱(直三棱柱指底面为三角形,侧棱与底面垂直的三棱柱)封闭容器内可以向各个方向自由运动,则该小球不可能接触到的容器内壁的面积是:( )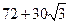
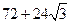
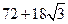
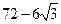
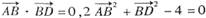 ,若将其沿BD折成直二面角A-BD-C,则A-BCD的外接球的表面积为
,若将其沿BD折成直二面角A-BD-C,则A-BCD的外接球的表面积为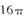 B
B 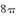 C
C 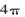 d.
d.