题目内容
下表是某年美国旧轿车价格的调查资料,今以x表示轿车的使用年数,y表示相应的年均价格,求y关于x的回归
方程.
方程.
| 使用年数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年均价格 y(美元) | 2 651 | 1 943 | 1 494 | 1 087 | 765 | 538 | 484 | 290 | 226 | 204 |
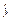 =e-0.298x+8.165
=e-0.298x+8.165作出散点图如图所示.
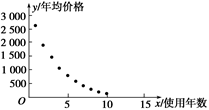
可以发现,各点并不是基本处于一条直线附近,因此,y与x之间应是非线性相关关系.与已学函数图象比较,用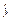 =e
=e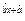 来刻画题中模型更为合理,令
来刻画题中模型更为合理,令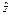 =ln
=ln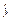 ,则
,则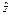 =
=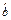 x+
x+ ,题中数据变成如下表所示:
,题中数据变成如下表所示:
相应的散点图如图所示,从图中可以看出,变换的样本点分布在一条直线附近,因此可以用线性回归方程拟合.
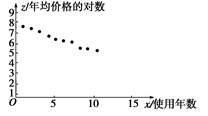
由表中数据可得r≈-0.996.|r|>r0.05.认为x与z之间具有线性相关关系,由表中数据得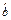 ≈-0.298,
≈-0.298,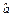 ≈8.165,所以
≈8.165,所以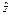 =-0.298x+8.165,最后回代
=-0.298x+8.165,最后回代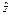 =ln
=ln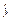 ,即
,即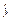 =e-0.298x+8.165为所求.
=e-0.298x+8.165为所求.

可以发现,各点并不是基本处于一条直线附近,因此,y与x之间应是非线性相关关系.与已学函数图象比较,用
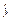 =e
=e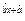 来刻画题中模型更为合理,令
来刻画题中模型更为合理,令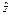 =ln
=ln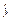 ,则
,则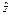 =
=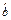 x+
x+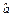 ,题中数据变成如下表所示:
,题中数据变成如下表所示:| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| z | 7.883 | 7.572 | 7.309 | 6.991 | 6.640 | 6.288 | 6.182 | 5.670 | 5.421 | 5.318 |

由表中数据可得r≈-0.996.|r|>r0.05.认为x与z之间具有线性相关关系,由表中数据得
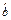 ≈-0.298,
≈-0.298,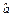 ≈8.165,所以
≈8.165,所以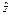 =-0.298x+8.165,最后回代
=-0.298x+8.165,最后回代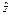 =ln
=ln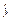 ,即
,即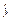 =e-0.298x+8.165为所求.
=e-0.298x+8.165为所求.
练习册系列答案
相关题目
 岁至
岁至 岁的身高,数据如下表,由此建立的身高与年龄的回归模型为
岁的身高,数据如下表,由此建立的身高与年龄的回归模型为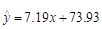 .用这个模型预测这个孩子
.用这个模型预测这个孩子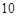 岁时的身高,则正确的叙述是
岁时的身高,则正确的叙述是 
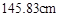 B.身高在
B.身高在 性别
性别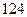 人,其中六十岁以上的
人,其中六十岁以上的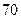 人,六十岁以下的
人,六十岁以下的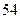 人,六十岁以上的人中有
人,六十岁以上的人中有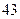 人的饮食以蔬菜为主,另外
人的饮食以蔬菜为主,另外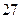 人则以肉类为主;六十岁以下的人中有
人则以肉类为主;六十岁以下的人中有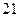 人饮食以蔬菜为主,另外
人饮食以蔬菜为主,另外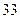 人则以肉类为主.(1)根据以上数据建立一个
人则以肉类为主.(1)根据以上数据建立一个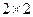 的列联表;(2)判断人的饮食习惯是否与年龄有关.
的列联表;(2)判断人的饮食习惯是否与年龄有关. 号电池
号电池 节,
节, 号电池
号电池 ;第二天收集
;第二天收集 节,
节, 节,总质量为
节,总质量为 .
.





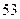



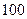 位居民进行调查,经过计算
位居民进行调查,经过计算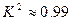 ,根据这一数据分析,下列说法正确的是 ( )
,根据这一数据分析,下列说法正确的是 ( )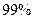 的人认为该栏目优秀
的人认为该栏目优秀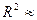 。
。