题目内容
若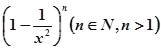 的展开式中
的展开式中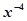 的系数为
的系数为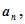
则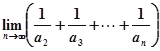 =
= .
.
2
解析试题分析:二项展开式通项为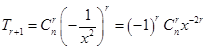 ,令
,令 得
得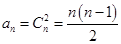
所以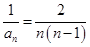
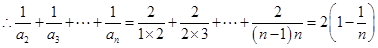 ,所以所求式子为
,所以所求式子为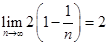
考点:二项式定理及数列求和求极限
点评:在二项式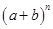 的展开式中任意一项可由
的展开式中任意一项可由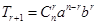 求得,数列求和是常考的知识点,本题采用的是裂项相消法求和,适用于通项为
求得,数列求和是常考的知识点,本题采用的是裂项相消法求和,适用于通项为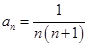 形式的数列
形式的数列

练习册系列答案
相关题目
在各项均为实数的等比数列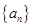 中,
中,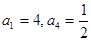 ,则
,则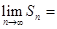 ( )
( )
| A.2 | B. 8 | C.16 | D.32 |
已知a<b<|a|,则( )
A. > >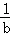 | B.ab<1 | C. >1 >1 | D.a2>b2 |
若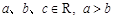 ,则下列不等式成立的是( ).
,则下列不等式成立的是( ).
A.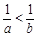 | B.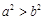 |
C.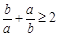 | D.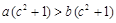 |
已知x=lnπ,y=log52,z=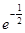 ,则( )
,则( )
| A.x<y<z | B.z<x<y | C.z<y<x | D.y<z<x |
若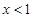 ,则下列关系中正确的是( )
,则下列关系中正确的是( )
A.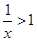 | B.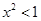 | C. | D. |
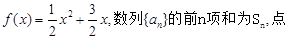
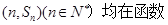
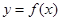
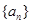 的通项公式
的通项公式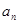 ;
; 求数列
求数列
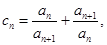 证明:
证明: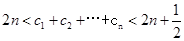 。
。 中,
中,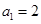 ,
,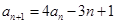 ,
,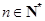 .
.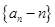 是等比数列;
是等比数列;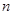 项和
项和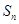 ;
;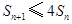 ,对任意
,对任意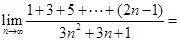 .
.