题目内容
(本小题满分12分) 等差数列![]() 中,首项
中,首项![]() ,公差
,公差![]() ,前n项和为
,前n项和为![]() ,已知数列
,已知数列![]() 成等比数列,其中
成等比数列,其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)令![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() .若存在一个最小正整数M,使得当
.若存在一个最小正整数M,使得当![]() 时,
时,![]() (
(![]() )恒成立,试求出这个最小正整数M的值.
)恒成立,试求出这个最小正整数M的值.
解:(Ⅰ)由,得![]() ,解得
,解得![]() ,
,![]() , 2分
, 2分
![]() ,又在等比数列中,公比
,又在等比数列中,公比![]() ,∴
,∴![]() ,
,
![]() ,
,![]() . 6分
. 6分
(Ⅱ)![]() ,
,
则![]() ,
,![]() ,两式相减得:
,两式相减得:
![]()
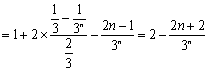 ,∴
,∴![]() . 8分
. 8分
∵![]() ,
,
∴![]() 单调递增,∴
单调递增,∴![]() .又
.又![]() 在
在![]() 时单调递增. 10分
时单调递增. 10分
且![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ;….
;….
故当![]() 时,
时,![]() 恒成立,则所求最小正整数M的值为3. 12分
恒成立,则所求最小正整数M的值为3. 12分

练习册系列答案
相关题目