题目内容
已知动⊙M经过点D(-2,0),且与圆C:x2+y2-4x=0外切.(1)求点M的轨迹方程;
(2)记半径最小的圆为⊙M,直线l与⊙M相交于A,B两点,且⊙M上存在点P,使得
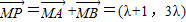 (λ≠0)
(λ≠0)①求⊙M的方程;
②求直线l的方程及相应的点P坐标.
【答案】分析:(1)利用两圆相外切的条件,结合双曲线的定义,求出双曲线的方程.
(2)①MD的最小值为c-a=1,且M(-1,0)写出方程.
②先求出点P坐标表达式,代入⊙M方程,求出点P的坐标,判断MAPB是菱形,求出AB斜率,及MP的中点,点斜式写出直线l的方程.
解答:解:(1)圆C半径R=2,圆心C(2,0),(1分)由题意可得,MC=MD+2,MC-MD=2<CD=4,(3分)
∴点M的轨迹是以C,D为焦点的双曲线的左支,其中2a=2,2c=4,∴a=1,c=2,∴b2=3.(5分)
∴点M的轨迹方程为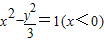 .(6分)
.(6分)
(2)①∵MD的最小值为c-a=1,且M(-1,0),∴⊙M的方程为(x+1)2+y2=1.(8分)
②由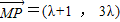 ,把点P(λ,3λ)代入⊙M:(x+1)2+y2=1,
,把点P(λ,3λ)代入⊙M:(x+1)2+y2=1,
解得 ,(10分)∴
,(10分)∴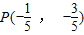 ,且
,且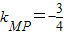 .(12分)
.(12分)
∵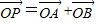 ,且
,且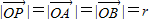 ,∴MAPB是菱形. (13分)
,∴MAPB是菱形. (13分)
∴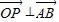 ,∴
,∴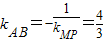 .
.
又MP的中点为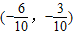 ,∴直线
,∴直线 ,
,
即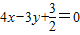 .(15分)
.(15分)
点评:本题考查轨迹方程的求法,直线和圆位置关系的综合应用,属于中档题.
(2)①MD的最小值为c-a=1,且M(-1,0)写出方程.
②先求出点P坐标表达式,代入⊙M方程,求出点P的坐标,判断MAPB是菱形,求出AB斜率,及MP的中点,点斜式写出直线l的方程.
解答:解:(1)圆C半径R=2,圆心C(2,0),(1分)由题意可得,MC=MD+2,MC-MD=2<CD=4,(3分)
∴点M的轨迹是以C,D为焦点的双曲线的左支,其中2a=2,2c=4,∴a=1,c=2,∴b2=3.(5分)
∴点M的轨迹方程为
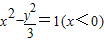 .(6分)
.(6分)(2)①∵MD的最小值为c-a=1,且M(-1,0),∴⊙M的方程为(x+1)2+y2=1.(8分)
②由
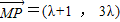 ,把点P(λ,3λ)代入⊙M:(x+1)2+y2=1,
,把点P(λ,3λ)代入⊙M:(x+1)2+y2=1,解得
 ,(10分)∴
,(10分)∴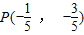 ,且
,且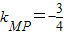 .(12分)
.(12分)∵
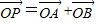 ,且
,且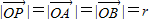 ,∴MAPB是菱形. (13分)
,∴MAPB是菱形. (13分)∴
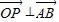 ,∴
,∴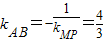 .
.又MP的中点为
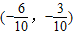 ,∴直线
,∴直线 ,
,即
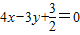 .(15分)
.(15分)点评:本题考查轨迹方程的求法,直线和圆位置关系的综合应用,属于中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 已知椭圆C经过点M(1,
已知椭圆C经过点M(1,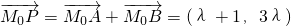 (λ≠0)
(λ≠0)