题目内容
(2012•芜湖三模)设两个复数集N={z|z=2cosθ+i(λ+3sinθ),θ∈R},M={z|z=t+i(4-t2),t∈R}的交集为非空集合,则实数λ的取值范围是( )
分析:由题设得
有解,所以λ=4-3sinθ-4cos2θ=4(sinθ-
)2-
,由此能求出实数λ的取值范围.
|
| 3 |
| 8 |
| 9 |
| 16 |
解答:解:∵N={z|z=2cosθ+i(λ+3sinθ),θ∈R},
M={z|z=t+i(4-t2),t∈R}的交集为非空集合,
∴
有解,
∴λ=4-3sinθ-4cos2θ
=-3sinθ+4sin2θ
=4(sin2θ-
sinθ)
=4(sinθ-
)2-
,
∴当sinθ=
时,λ取最小值-
,
当sinθ=-1时,λ取最大值7,
故选D.
M={z|z=t+i(4-t2),t∈R}的交集为非空集合,
∴
|
∴λ=4-3sinθ-4cos2θ
=-3sinθ+4sin2θ
=4(sin2θ-
| 3 |
| 4 |
=4(sinθ-
| 3 |
| 8 |
| 9 |
| 16 |
∴当sinθ=
| 3 |
| 8 |
| 9 |
| 16 |
当sinθ=-1时,λ取最大值7,
故选D.
点评:本题考查方程思想、函数思想、分离参数的思想方法.考查分析、解决、逻辑思维、计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
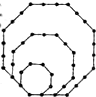 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是