题目内容
(本题14分)已知圆 和点
和点
(1)若过点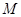 有且只有一条直线与圆
有且只有一条直线与圆 相切,求实数
相切,求实数 的值,并求出切线方程;
的值,并求出切线方程;
(2)若 ,过点
,过点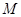 作圆的两条弦
作圆的两条弦 ,且
,且 互相垂直,求
互相垂直,求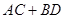 的最大值。
的最大值。
【答案】
(1) 或即
或即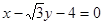 。(2)
。(2)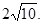
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)因为圆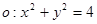 和点
和点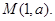 ,若过点
,若过点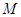 有且只有一条直线与圆
有且只有一条直线与圆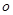 相切,则联立方程组只有一个实数解得到切线方程。
相切,则联立方程组只有一个实数解得到切线方程。
(2)若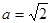 ,过点
,过点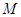 作圆的两条弦
作圆的两条弦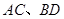 ,且
,且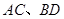 互相垂直,设
互相垂直,设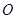 到直线
到直线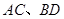 的距离分别为
的距离分别为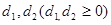 ,则
,则 于是
于是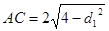 ,
,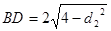 ,所以
,所以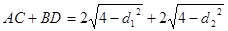 则
则 ,则利用不等式得到结论。
,则利用不等式得到结论。
解:(1)由条件知点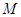 在圆
在圆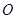 上,所以
上,所以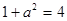 ,则
,则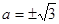 。当
。当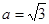 时,点
时,点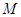 为
为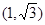 ,
,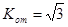 ,
,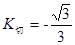 此时切线方程为
此时切线方程为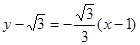 ,即
,即 。当
。当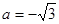 时,点
时,点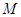 为
为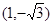 ,
,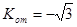 ,
, 此时切线方程为
此时切线方程为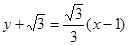 ,即
,即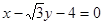 。所以所求的切线方程为
。所以所求的切线方程为 或即
或即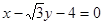 。-------------6分
。-------------6分
(2)设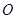 到直线
到直线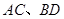 的距离分别为
的距离分别为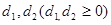 ,则
,则 于是
于是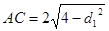 ,
,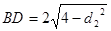 ,所以
,所以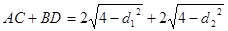 则
则 ,因为
,因为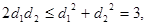 ,所以
,所以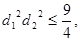 ,当且仅当
,当且仅当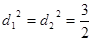 时取等号,所以
时取等号,所以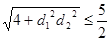 ,所以
,所以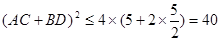 ,所以
,所以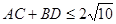 ,即
,即
的最大值为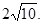 --------------------14分
--------------------14分

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
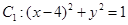 ,圆
,圆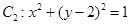 ,动点
,动点 到圆
到圆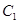 ,
,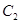 上点的距离的最小值相等.
上点的距离的最小值相等. ,使得点
,使得点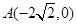 的距离减去点
的距离减去点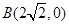 的距离的差为
的距离的差为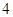 ,如果存在求出
,如果存在求出 内有一点
内有一点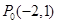 ,AB为过点
,AB为过点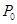 且倾斜角为α的弦,
且倾斜角为α的弦,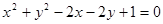 相切的直线
相切的直线 交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).
交x轴、y轴于A、B两点,O为原点,|OA|=3,|OB|=b(b>2).