题目内容
已知函数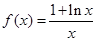 .
.
(1)若函数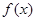 在区间
在区间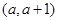 上有极值,求实数
上有极值,求实数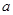 的取值范围;
的取值范围;
(2)若关于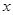 的方程
的方程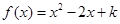 有实数解,求实数
有实数解,求实数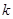 的取值范围;
的取值范围;
(3)当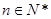 ,
,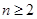 时,求证:
时,求证: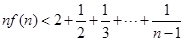 .
.
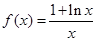 .
.(1)若函数
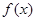 在区间
在区间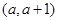 上有极值,求实数
上有极值,求实数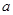 的取值范围;
的取值范围;(2)若关于
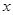 的方程
的方程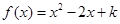 有实数解,求实数
有实数解,求实数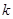 的取值范围;
的取值范围;(3)当
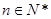 ,
,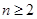 时,求证:
时,求证: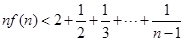 .
.(1)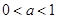
(2)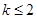
(3)根据数列的求和来放缩法得到不等式的证明关键是对于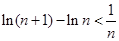 的运用。
的运用。
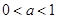
(2)
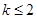
(3)根据数列的求和来放缩法得到不等式的证明关键是对于
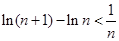 的运用。
的运用。试题分析:解:(1)
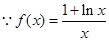 ,
,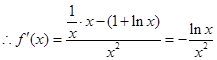
 当
当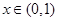 时,
时,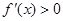 ;当
;当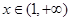 时,
时,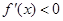 ;
; 函数
函数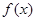 在区间(0,1)上为增函数;在区间
在区间(0,1)上为增函数;在区间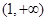 为减函数 3分
为减函数 3分 当
当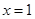 时,函数
时,函数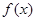 取得极大值,而函数
取得极大值,而函数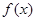 在区间
在区间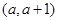 有极值.
有极值.
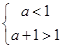 ,解得
,解得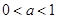 . 5分
. 5分(2)由(1)得
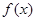 的极大值为
的极大值为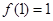 ,令
,令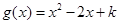 ,所以当
,所以当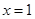 时,函数
时,函数 取得最小值
取得最小值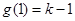 ,又因为方程
,又因为方程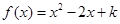 有实数解,那么
有实数解,那么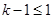 ,即
,即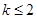 ,所以实数
,所以实数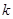 的取值范围是:
的取值范围是: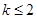 . 10分
. 10分(另解:
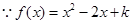 ,
, ,
,令
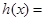
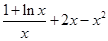 ,所以
,所以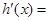
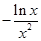
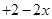 ,当
,当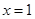 时,
时,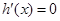
当
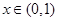 时,
时,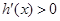 ;当
;当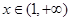 时,
时,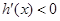
 当
当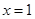 时,函数
时,函数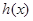 取得极大值为
取得极大值为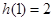
 当方程
当方程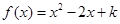 有实数解时,
有实数解时,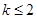 .)
.)(3)
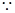 函数
函数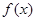 在区间
在区间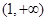 为减函数,而
为减函数,而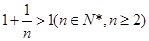 ,
,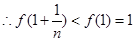
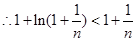 ,即
,即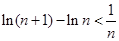
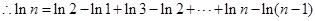
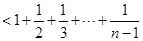 12分
12分即
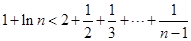 ,
,而
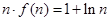 ,
,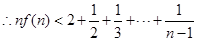 结论成立. 16分
结论成立. 16分点评:根据导数的符号判定函数的单调性,是解决该试题的关键,同时能结合函数与方程的思想求解方程的根,属于中档题。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 满足
满足 ,
,  (
( ),则
),则 =
= 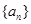 的前
的前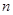 项和为
项和为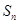 ,点
,点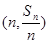 在直线
在直线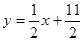 上.数列
上.数列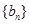 满足
满足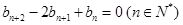 ,且
,且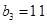 ,前9项和为153.
,前9项和为153.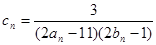 ,数列
,数列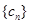 的前
的前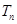 ,求使不等式
,求使不等式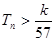 对一切
对一切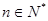 都成立的最大正整数
都成立的最大正整数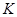 的值;
的值;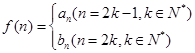 ,问是否存在
,问是否存在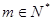 ,使得
,使得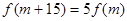 成立?若存在,求出
成立?若存在,求出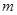 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.  为等差数列,若
为等差数列,若 ,则
,则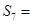 .
.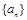 满足
满足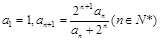 .
.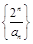 是等差数列;
是等差数列;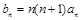 ,求数列
,求数列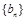 的前
的前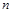 项和
项和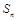 .
. 的前六项和为60,且
的前六项和为60,且 的等比中项.(Ⅰ)求数列
的等比中项.(Ⅰ)求数列 ;(Ⅱ)若数列
;(Ⅱ)若数列 的前
的前 项和
项和
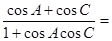 。
。 的前
的前 项的和为
项的和为 ,且
,且 ,则
,则 ( )
( ) 而言,若
而言,若 是以
是以 为公差的等差数列,
为公差的等差数列,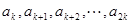 是以
是以 为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知
为公差的等差数列,依此类推,我们就称该数列为等差数列接龙,已知 ,则
,则 等于
等于