题目内容
在直角坐标系xoy中,曲线C1上的点均在C2:(x-5)2+y2=9外,且对C1上任意一点M,M到直线x=-2的距离等于该点与圆C2上点的距离的最小值.(Ⅰ)求曲线C1的方程
(Ⅱ)设P(x,y)(y≠±3)为圆C2外一点,过P作圆C2的两条切线,分别于曲线C1相交于点A,B和C,D.证明:当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值.
【答案】分析:(Ⅰ)设M的坐标为(x,y),根据对C1上任意一点M,M到直线x=-2的距离等于该点与圆C2上点的距离的最小值,可得|x+2|=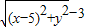 且圆C2上的点位于直线x=-2的右侧,从而可得曲线C1的方程;
且圆C2上的点位于直线x=-2的右侧,从而可得曲线C1的方程;
(Ⅱ)当点P在直线x=-4上运动时,P的坐标为(-4,y),设切线方程为kx-y+y+4k=0,利用直线与圆相切可得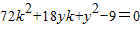 ,从而可得过P所作的两条切线PA,PC的斜率k1,k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,从而可得
,从而可得过P所作的两条切线PA,PC的斜率k1,k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,从而可得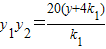 ;同理可得
;同理可得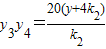 ,由此可得当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
,由此可得当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
解答:(Ⅰ)解:设M的坐标为(x,y),由已知得|x+2|=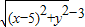 且圆C2上的点位于直线x=-2的右侧
且圆C2上的点位于直线x=-2的右侧
∴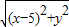 =x+5
=x+5
化简得曲线C1的方程为y2=20x
(Ⅱ)证明:当点P在直线x=-4上运动时,P的坐标为(-4,y),
∵y≠±3,∴过P且与圆C2相切的直线的斜率k存在且不为0,每条切线都与抛物线有两个交点,切线方程为
y-y=k(x+4),即kx-y+y+4k=0,
∴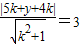 ,整理得
,整理得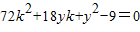 ①
①
设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1,k2是方程①的两个实根
∴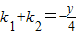 ②
②
由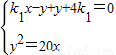 ,消元可得
,消元可得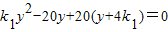 ③
③
设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,
∴y1,y2是方程③的两个实根
∴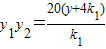 ④
④
同理可得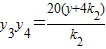 ⑤
⑤
由②④⑤可得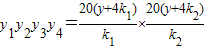 =
=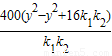 =6400
=6400
∴当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
点评:本题考查轨迹方程,考查直线与圆相切,考查韦达定理的运用,解题的关键是切线与抛物线联立,属于中档题.
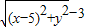 且圆C2上的点位于直线x=-2的右侧,从而可得曲线C1的方程;
且圆C2上的点位于直线x=-2的右侧,从而可得曲线C1的方程;(Ⅱ)当点P在直线x=-4上运动时,P的坐标为(-4,y),设切线方程为kx-y+y+4k=0,利用直线与圆相切可得
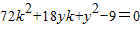 ,从而可得过P所作的两条切线PA,PC的斜率k1,k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,从而可得
,从而可得过P所作的两条切线PA,PC的斜率k1,k2是方程的两个实根,设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,从而可得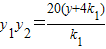 ;同理可得
;同理可得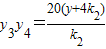 ,由此可得当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
,由此可得当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.解答:(Ⅰ)解:设M的坐标为(x,y),由已知得|x+2|=
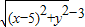 且圆C2上的点位于直线x=-2的右侧
且圆C2上的点位于直线x=-2的右侧∴
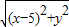 =x+5
=x+5化简得曲线C1的方程为y2=20x
(Ⅱ)证明:当点P在直线x=-4上运动时,P的坐标为(-4,y),
∵y≠±3,∴过P且与圆C2相切的直线的斜率k存在且不为0,每条切线都与抛物线有两个交点,切线方程为
y-y=k(x+4),即kx-y+y+4k=0,
∴
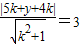 ,整理得
,整理得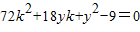 ①
①设过P所作的两条切线PA,PC的斜率分别为k1,k2,则k1,k2是方程①的两个实根
∴
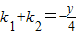 ②
②由
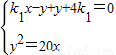 ,消元可得
,消元可得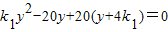 ③
③设四点A,B,C,D的纵坐标分别为y1,y2,y3,y4,
∴y1,y2是方程③的两个实根
∴
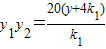 ④
④同理可得
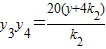 ⑤
⑤由②④⑤可得
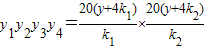 =
=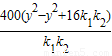 =6400
=6400∴当P在直线x=-4上运动时,四点A,B,C,D的纵坐标之积为定值为6400.
点评:本题考查轨迹方程,考查直线与圆相切,考查韦达定理的运用,解题的关键是切线与抛物线联立,属于中档题.

练习册系列答案
相关题目
 如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为
如图所示,在直角坐标系xOy中,射线OA在第一象限,且与x轴的正半轴成定角60°,动点P在射线OA上运动,动点Q在y轴的正半轴上运动,△POQ的面积为