题目内容
| |||||||||||||||
解析:
(1) |
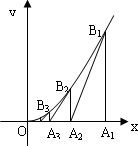
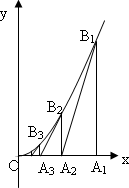
解:曲线C在Bn(an,bn)的切线BnAn+1斜率为:
kn= 又∵kn= ∴ ∴{an}为等比数列,公比为 ∴{an}的通项an= |
(2) |
由(Ⅰ)知bn= ∴Sn= ∴ 解得:32< |
(3) |
解:由(Ⅱ)知,数列{Sn}是等比数列,首项S1= ∴Tn= ∴ ∴Tn=1- ∴8ncn=(8ncn-8n-1cn-1)+(8n-1cn-1-8n-2cn-2)+…+(83c3-82c2)+(82c2-8c1)+8c1 =(8n-1-1)+(8n-2-1)+…(82-1)+(8-1)+8c1 = ∴所求通项cn= [评析]:在等差数列中,若 |

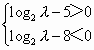
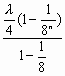 =
=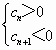 则只有前n项和Tn最大,若
则只有前n项和Tn最大,若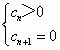 则Tn与Tn+1同时达到最大;理科第(Ⅲ)题解题关键是构造数列{8ncn},并用迭加
则Tn与Tn+1同时达到最大;理科第(Ⅲ)题解题关键是构造数列{8ncn},并用迭加
 +
+ =1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且|
=1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且| |,|
|,| |,|
|,| |成等比数列.又点N满足
|成等比数列.又点N满足 =
= (
( +
+ ),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M. ·
· =
=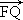 ,且|
,且| ,求椭圆方程.
,求椭圆方程.


