Question

若实数a，b，c满足2^a=-a，log

1

2

b=b，log₂c=（

1

2

）^c（　　）

A．a＜b＜c

B．a＜c＜b

C．c＜a＜b

D．b＜c＜a

Answer 1

分析：题目给出的a、b、c是三个方程的根，把每个方程转化为两个函数的零点，借助于图象即可比较三个实数的大小．

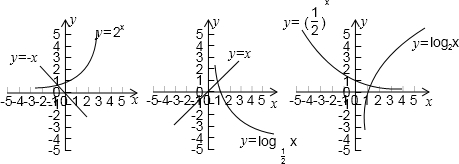
解答：解：a是方程2^a=-a的解，即为两个函数y=2^x与y=-x的交点的横坐标；
b是方程log

1

2

b=b的解，即为两个函数y=log

1

2

x与y=x的交点的横坐标；
c是方程log₂c=(

1

2

)c的解，即为两个函数y=log₂x与y=(

1

2

)x的交点的横坐标．
由图可得：a＜b＜c．
故选A．

点评：本题考查了三个实数的大小比较，考查了方程思想和数学转化思想，数形结合思想，解答此题的关键是把方程的根转化为两个函数图象的交点，题目设置新颖．