题目内容
(2013•兰州一模)定义:min{a,b}=
.在区域
内任取一点P(x,y),则x、y满足min{x2+x+2y,x+y+4}=x2+x+2y的概率为( )
|
|
分析:本题是一个几何概型,试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},算出两个集合对应的面积,面积之比就是要求的概率.
解答: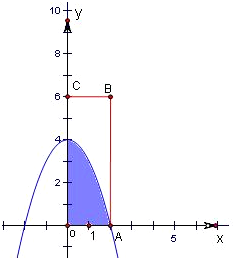 解:本题是一个几何概型,
解:本题是一个几何概型,
∵试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},
∴SΩ=1×1=1,
∵满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},即A={(x,y)|0≤x≤2,0≤y≤6,y≤4-x2},
∴SA=
(4-x2)dx=(4x-
x3)|
=
,
∴由几何概型公式得到P=
=
.
故选B.
 解:本题是一个几何概型,
解:本题是一个几何概型,∵试验包含的所有事件对应的集合Ω={(x,y)|0≤x≤2,0≤y≤6},
∴SΩ=1×1=1,
∵满足条件的事件A={(x,y)|0≤x≤2,0≤y≤6,x2+x+2y≤x+y+4},即A={(x,y)|0≤x≤2,0≤y≤6,y≤4-x2},
∴SA=
| ∫ | 2 0 |
| 1 |
| 3 |
2 0 |
| 16 |
| 3 |
∴由几何概型公式得到P=
| ||
| 2×6 |
| 4 |
| 9 |
故选B.
点评:本题以二元一次不等式组表示的平面区域为例,求几何概型的概率,着重考查了简单线性规划和几何概型的概率求法等知识,属于基础题.

练习册系列答案
相关题目