题目内容
 如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2| 2 |
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
(3)求四面体PEFC的体积.
分析:(1)设G为PC的中点,连接FG,EG,根据中位线定理得到FG
CD,AE
CD,进而可得到AF∥GE,再由线面平行的判定定理可证明AF∥平面PCE,得证.
(2)根据PA=AD=2可得到AF⊥PD,再由线面垂直的性质定理可得到PA⊥CD,然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD,同样得到GE⊥平面PCD,再由面面垂直的判定定理可得证.
(3)先由(2)可得知EG为四面体PEFC的高,进而求出S△PCF,根据棱锥的体积公式可得到答案.
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
(2)根据PA=AD=2可得到AF⊥PD,再由线面垂直的性质定理可得到PA⊥CD,然后由AD⊥CD结合线面垂直的判定定理得到CD⊥平面PAD,同样得到GE⊥平面PCD,再由面面垂直的判定定理可得证.
(3)先由(2)可得知EG为四面体PEFC的高,进而求出S△PCF,根据棱锥的体积公式可得到答案.
解答: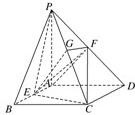 解:(1)证明:设G为PC的中点,连接FG,EG,
解:(1)证明:设G为PC的中点,连接FG,EG,
∵F为PD的中点,E为AB的中点,
∴FG
CD,AE
CD
∴FG
AE,∴AF∥GE
∵GE?平面PEC,
∴AF∥平面PCE;
(2)证明:∵PA=AD=2,∴AF⊥PD
又∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
∵AF?平面PAD,∴AF⊥CD.
∵PD∩CD=D,∴AF⊥平面PCD,
∴GE⊥平面PCD,
∵GE?平面PEC,
∴平面PCE⊥平面PCD;
(3)由(2)知,GE⊥平面PCD,
所以EG为四面体PEFC的高,
又GF∥CD,所以GF⊥PD,
EG=AF=
,GF=
CD=
,
S△PCF=
PD•GF=2.
得四面体PEFC的体积V=
S△PCF•EG=
.
 解:(1)证明:设G为PC的中点,连接FG,EG,
解:(1)证明:设G为PC的中点,连接FG,EG,∵F为PD的中点,E为AB的中点,
∴FG
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
∴FG
| ||
. |
∵GE?平面PEC,
∴AF∥平面PCE;
(2)证明:∵PA=AD=2,∴AF⊥PD
又∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
∵AF?平面PAD,∴AF⊥CD.
∵PD∩CD=D,∴AF⊥平面PCD,
∴GE⊥平面PCD,
∵GE?平面PEC,
∴平面PCE⊥平面PCD;
(3)由(2)知,GE⊥平面PCD,
所以EG为四面体PEFC的高,
又GF∥CD,所以GF⊥PD,
EG=AF=
| 2 |
| 1 |
| 2 |
| 2 |
S△PCF=
| 1 |
| 2 |
得四面体PEFC的体积V=
| 1 |
| 3 |
2
| ||
| 3 |
点评:本题主要考查线面垂直的判定定理和性质定理、面面垂直的判定定理.考查对立体几何中基本定理的掌握程度和灵活运用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
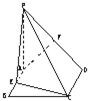 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点. 如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点
如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点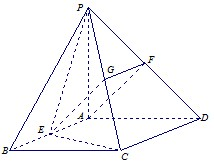 如图,PA垂直于矩形ABCD所在平面,PA=AD,E、F分别是AB、PD的中点.
如图,PA垂直于矩形ABCD所在平面,PA=AD,E、F分别是AB、PD的中点. 如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,