题目内容
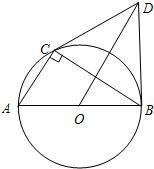11、如图，⊙O是Rt△ABC的外接圆，点O在AB上，BD⊥AB，点B是垂足，OD∥AC，连接CD．求证：CD是⊙O的切线．
分析：连接CO，先证△COD≌△BOD，从而求得∠OCD=∠OBD=90°即得到了CD是⊙O的切线．
解答：
证明：连接CO，（1分）
∵OD∥AC，
∴∠COD=∠ACO，∠CAO=∠DOB．（3分）
∵∠ACO=∠CAO，
∴∠COD=∠DOB．（6分）
∵OD=OD，OC=OB，
∴△COD≌△BOD．（8分）
∴∠OCD=∠OBD=90°．
∴OC⊥CD，即CD是⊙O的切线．（10分）
证明：连接CO，（1分）∵OD∥AC，
∴∠COD=∠ACO，∠CAO=∠DOB．（3分）
∵∠ACO=∠CAO，
∴∠COD=∠DOB．（6分）
∵OD=OD，OC=OB，
∴△COD≌△BOD．（8分）
∴∠OCD=∠OBD=90°．
∴OC⊥CD，即CD是⊙O的切线．（10分）
点评：本题主要考查了圆的切线的性质定理的证明，涉及圆的切线和全等三角形的判定的综合运用．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
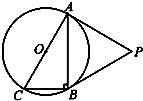如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
（A）（几何证明选讲选做题）如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径作圆与斜边AB交于点D，则BD的长为=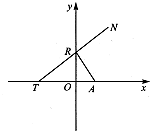
如图所示，点A（p，o）（p＞0），点R在y轴上运动，点T在x轴上，N为动点，且
，BC=1，求⊙O的半径．
，BC=1，求⊙O的半径．