题目内容
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;
(2)已知PA=
 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.
【答案】分析:(1)要证PB是⊙O的切线,只要连接OB,求证∠OBP=90°即可;
(2)连接OP,交AB于点D,求半径时,可以证明△APO∽△DPA,还可证明△PAO∽△ABC,在Rt△OAP中利用勾股定理.
解答:证明:(1)连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.(2分)
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.(4分)
又∵OB是⊙O半径,
∴PB是⊙O的切线,(5分)
(2)解:连接OP,交AB于点D ,
,
∵PA=PB,
∴点P在线段AB的垂直平分线上.
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,(7分)
∴∠PAO=∠PDA=90°.
又∵∠APO=∠DPA,
∴△APO∽△DPA,
∴ ,
,
∴AP2=PO•DP.
又∵OD= BC=
BC= ,
,
∴PO(PO-OD)=AP2,
即:PO2- PO=
PO= ,
,
解得PO=2,(9分)
在Rt△APO中, ,即⊙O的半径为1.(10分)
,即⊙O的半径为1.(10分)
点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.同时考查了相似三角形的判定和性质,及勾股定理的运用.
(2)连接OP,交AB于点D,求半径时,可以证明△APO∽△DPA,还可证明△PAO∽△ABC,在Rt△OAP中利用勾股定理.
解答:证明:(1)连接OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,
∴∠PAO=∠PBO.(2分)
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB.(4分)
又∵OB是⊙O半径,
∴PB是⊙O的切线,(5分)
(2)解:连接OP,交AB于点D
 ,
,∵PA=PB,
∴点P在线段AB的垂直平分线上.
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,(7分)
∴∠PAO=∠PDA=90°.
又∵∠APO=∠DPA,
∴△APO∽△DPA,
∴
 ,
,∴AP2=PO•DP.
又∵OD=
 BC=
BC= ,
,∴PO(PO-OD)=AP2,
即:PO2-
 PO=
PO= ,
,解得PO=2,(9分)
在Rt△APO中,
 ,即⊙O的半径为1.(10分)
,即⊙O的半径为1.(10分)点评:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.同时考查了相似三角形的判定和性质,及勾股定理的运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
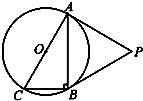 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. (A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
(A)(几何证明选讲选做题)如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=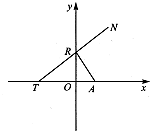 如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且
如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.