题目内容
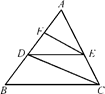
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。
求:(1)⊙O的半径;
(2)s1n∠BAP的值。
(1)7.5(2)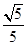
解析试题分析:(1)由题可知,利用切割线定理即可;(2)根据弦切角定理可知s1n∠BAP=s1n∠ACB,然后求出AB、BC的比值即可.
试题解析:(1)因为PA为⊙O的切线,所以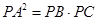 ,
,
又由PA=10,PB=5,所以PC=20,BC=20-5=15 2分.
因为BC为⊙O的直径,所以⊙O的半径为7.5. 4分
(2)∵PA为⊙O的切线,∴∠ACB=∠PAB, 5分
又由∠P=∠P, ∴△PAB∽△PCA,∴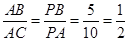 7分
7分
设AB=k,AC="2k," ∵BC为⊙O的直径,
∴AB⊥AC∴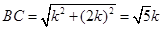 8分
8分
∴s1n∠BAP=s1n∠ACB=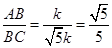 10分
10分
考点:平面几何中圆的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 是的∠A的平分线,圆
是的∠A的平分线,圆 经过点
经过点 与
与 切于点
切于点 ,与
,与 相交于
相交于 ,连结
,连结 ,
, .
. ; (2)求证:
; (2)求证: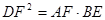 .
.
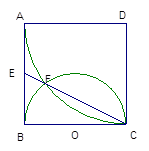
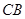 是⊙
是⊙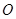 的直径,
的直径, 是⊙
是⊙ ,
,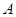 为切点.若
为切点.若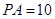 ,
, ,
, 的平分线
的平分线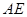 与
与 和⊙
和⊙ 、
、 ,求
,求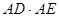 的值.
的值.
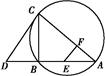
 PD.求CD的长.
PD.求CD的长.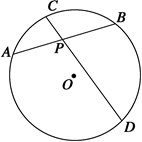
 于F(不与B重合),直线
于F(不与B重合),直线 与
与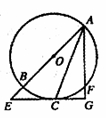
 ;(2)
;(2) .
. ,求AF的长.
,求AF的长.