题目内容
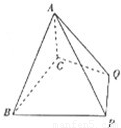
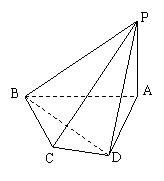
 如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.
如图,四棱锥A-BCDE中,△ABC是正三角形,四边形BCDE是矩形,且平面ABC⊥平面BCDE,AB=2,AD=4.(Ⅰ) 若点G是AE的中点,求证:AC∥平面BDG;
(II)若点F为线段AB的中点,求二面角B-CE-F的正切值.
分析:(Ⅰ)利用三角形的中位线定理和线面平行的判定定理即可证明;
(2)利用线面垂直的判定和性质定理、面面垂直的性质定理、二面角的定义即可得出.
(2)利用线面垂直的判定和性质定理、面面垂直的性质定理、二面角的定义即可得出.
解答:(Ⅰ)证明:连接CE、BD,设CE∩BD=O,连接OG,由三角形的中位线定理可得:OG∥AC,
∵AC?平面BDG,OG?平面BDG,
∴AC∥平面BDG.
(Ⅱ)∵平面ABC⊥平面BCDE,DC⊥BC,∴DC⊥平面ABC,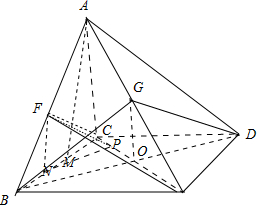
∴DC⊥AC,
在Rt△ACD中,CD=
=
=2
.
取BC的中点M,连接AM,则AM⊥平面BCDE.
取BM 的中点N,连接FN,则FN∥AM,∴FN⊥平面BCDE.
过点N作NP⊥CE,垂足为P,连接FP,由三垂线定理可得FP⊥CE.
∴∠FPN为二面角B-CE-F的平面角.
在Rt△CNP中,NP=CNsin∠NCP=
×
=
.
在Rt△FNP中,tan∠FPN=
=
=
.
∵AC?平面BDG,OG?平面BDG,
∴AC∥平面BDG.
(Ⅱ)∵平面ABC⊥平面BCDE,DC⊥BC,∴DC⊥平面ABC,

∴DC⊥AC,
在Rt△ACD中,CD=
| AD2-AC2 |
| 42-22 |
| 3 |
取BC的中点M,连接AM,则AM⊥平面BCDE.
取BM 的中点N,连接FN,则FN∥AM,∴FN⊥平面BCDE.
过点N作NP⊥CE,垂足为P,连接FP,由三垂线定理可得FP⊥CE.
∴∠FPN为二面角B-CE-F的平面角.
在Rt△CNP中,NP=CNsin∠NCP=
| 3 |
| 2 |
2
| ||||
|
3
| ||
| 4 |
在Rt△FNP中,tan∠FPN=
| FN |
| NP |
| ||||
|
| 2 |
| 3 |
点评:熟练掌握三角形的中位线定理、线面平行的判定定理、线面及面面垂直的判定和性质定理、二面角的定义是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
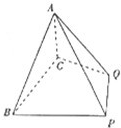 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=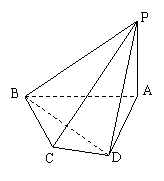
 BC,AB=AC=
BC,AB=AC=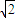 B.
B.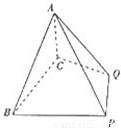
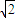 BC,AB=AC=
BC,AB=AC=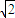 B.
B.